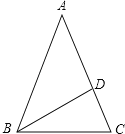
题目内容
【题目】在![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
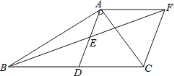
![]() 求证:
求证:![]() ;
;
![]() 当
当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是菱形,并证明.
是菱形,并证明.
【答案】![]() 证明见解析;
证明见解析; ![]() 是直角三角形时,四边形
是直角三角形时,四边形![]() 是菱形,理由见解析.
是菱形,理由见解析.
【解析】
(1)根据线段中点的定义可得AE=DE,根据“两直线平行,内错角相等”可得∠EAF=∠EDB,然后利用“角边角”证明△AEF和△DEB全等;
(2)根据全等三角形对应边相等可得AF=BD,根据直角三角形斜边上的中线等于斜边的一半求出AD=BD=CD,再根据一组对边平行且相等的四边形是平行四边形求出四边形ADCF是平行四边形,然后根据邻边相等的平行四边形是菱形证明即可.
![]() 证明:∵
证明:∵![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,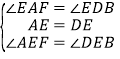 ,
,
∴![]() ;
;
![]() 解:
解:![]() 是直角三角形时,四边形
是直角三角形时,四边形![]() 是菱形.
是菱形.
理由如下:∵![]() ,
,
∴![]() ,
,
∵![]() 是直角三角形,
是直角三角形,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
∴四边形![]() 是菱形.
是菱形.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目