Question

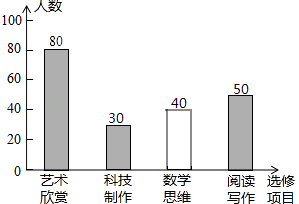
【题目】某校为了解“课程选修”的情况，对报名参加“艺术鉴赏”，“科技制作”，“数学思维”，“阅读写作”这四个选修项目的学生（每人限报一课）进行抽样调查，下面是根据收集的数据绘制的不完整的统计图：
请根据图中提供的信息，解答下面的问题：
（1）此次共调查了名学生，扇形统计图中“艺术鉴赏”部分的圆心角是度；
（2）请把这个条形统计图补充完整；
（3）现该校共有800名学生报名参加这四个选修项目，请你估计其中有多少名学生选修“科技制作”项目．

Answer 1

【答案】
（1）200；144
（2）解：数学思维的人数是：200﹣80﹣30﹣50=40（名），

补图如下：

（3）解：根据题意得：800× =120（名），

答：其中有120名学生选修“科技制作”项目

【解析】解：根据题意得： 调查的总学生数是：50÷25%=200（名），
“艺术鉴赏”部分的圆心角是 ×360°=144°；
故答案为：200，144；
（1）根据阅读写作的人数和所占的百分比，即可求出总学生数，再用艺术鉴赏的人数除以总人数乘以360°，即可得出答案；（2）用总学生数减去“艺术鉴赏”，“科技制作”，“阅读写作”，得出“数学思维”的人数，从而补全统计图；（3）用“科技制作”所占的百分比乘以总人数8000，即可得出答案．