题目内容
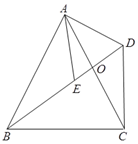
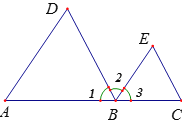
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,请证明:BD=AB﹣AF;
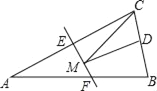
(2)试探索:点D在AB的延长线或反向延长线上时,请在备用图中画出图形,(1)中的结论是否成立?若不成立,请直接写出正确结论(不需要证明).
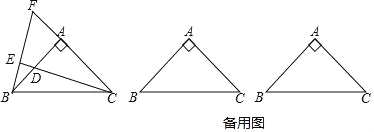
【答案】(1)证明见解析(2)结论不成立
【解析】
(1)易证∠FBA=∠FCE,结合条件容易证到△FAB≌△DAC,从而有FA=DA,就可得到AB=AD+BD=FA+BD.
(2)由于点D的位置在变化,因此线段AF、BD、AB之间的大小关系也会相应地发生变化,只需画出图象并借鉴(1)中的证明思路就可解决问题.
(1)证明∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°,
∴∠FBA=∠FCE,
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC,
在△FAB和△DAC中, ,
,
∴△FAB≌△DAC(ASA),
∴FA=DA,
∴AB=AD+BD=FA+BD,
∴BD=AB-AF;
(2)解:(1)中的结论不成立.
点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF.
理由如下:
①当点D在AB的延长线上时,如图2.

同理可得:FA=DA.
则AB=AD-BD=AF-BD.
②点D在AB的反向延长线上时,如图3.

同理可得:FA=DA.
则AB=BD-AD=BD-AF.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目