题目内容
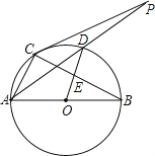
【题目】(1)在平面直角坐标系中A(5,0),B为y轴上任意一点,以点B为直角顶点作等腰Rt△ABC(点A、B、C按顺时针方向排列),请探究点C是否在一确定的直线上;
(2)在平面直角坐标系中,A(﹣1,0),B(4,2m),连接AB,将AB绕点B逆时针旋转90°到CB,请探究点C是否在一确定的直线上.
【答案】(1)见解析;(2)见解析.
【解析】
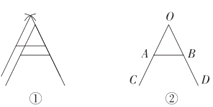
(1)如图1中,在y轴的正半轴上取一点D,使得OD=OA=5,证明△OAB∽△DAC,推出∠CDA=90°即可解决问题.
(2)如图2中,点B在直线x=4上,取一点D,使得DH=AH=1,证明△HAB∽△DAC,推出∠ADC=∠AHB=90°,即可解决问题.
解:(1)如图1中,在y轴的正半轴上取一点D,使得OD=OA=5,
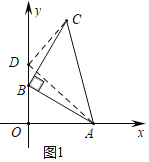
∵OD=OA,∠AOD=90°,
∴∠OAD=45°,
∵∠CAB=45°,
∴∠OAD=∠CAB,
∴∠OAB=∠DAC,
∵![]() =
=![]() =
=![]() ,
,
∴△OAB∽△DAC,
∴∠AOB=∠ADC=90°,
∴∠ODC=135°,
∴直线CD的解析式为y=x+5,
∴C是在一确定的直线上;
(2)如图2中,点B在直线x=4上,取一点D,使得DH=AH=1,
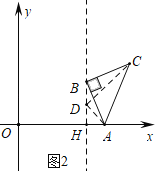
同法可证:△HAB∽△DAC,
∴∠ADC=∠AHB=90°,
∴∠CDH=135°,
∴直线CD的解析式为y=x﹣3,
∴点C在一确定的直线上.

【题目】某宾馆有若干间标准房,当标准房的价格为![]() 元时,每天入住的国间数为
元时,每天入住的国间数为![]() 间,经市场调查表明,该宾馆每间标准房的价格在
间,经市场调查表明,该宾馆每间标准房的价格在![]() 元之间(含
元之间(含![]() 元,
元,![]() 元)浮动时,每天人住的房间数
元)浮动时,每天人住的房间数![]() (间)与每间标准房的价格
(间)与每间标准房的价格![]() (元)的数据如下表:
(元)的数据如下表:
| …… | 190 | 200 | 210 | 220 | …… |
| …… | 65 | 60 | 55 | 50 | …… |
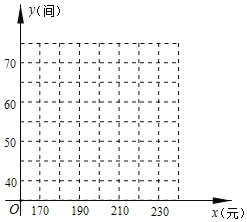
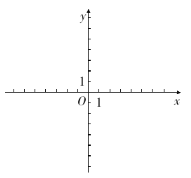
(1)根据所给数据在坐标系中描出相应的点,并画出图象.
(2)猜想(1)中的图象是什么函数的图象,求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围.
的取值范围.
(3)设客房的日营业额为W (元).若不考虑其他因素,问宾馆标准房的价格定为多少元时,客房的日营业额最大?最大为多少元?