题目内容
【题目】已知抛物线y=2x2+4x+k﹣1(k为大于2的正整数)与x轴有交点.
(1)求k的值及抛物线y=2x2+4x+k﹣1的对称轴;
(2)将抛物线y=2x2+4x+k﹣1在直线y=2上方的部分沿直线y=2翻折,其余部分不变,得到一个新图象,当直线y=![]() x+b与此图象有两个公共点时,求b的取值范围.
x+b与此图象有两个公共点时,求b的取值范围.
【答案】(1)k=3;x=﹣1;(2)2<b<3或b<![]()
【解析】
(1)令y=0,由一元二次方程根的判别式,即可求出k的取值范围,庵后得到k的值;由抛物线的对称轴公式,即可求出对称轴;
(2)根据题意,画出翻折后的图形,然后找出有两个函数有两个交点的临界点,求出临界点是b的值,然后即可得到b的取值范围.
解:(1)∵抛物线y=2x2+4x+k-1与x轴有交点,
∴42-4![]() 2(k-1)=24-8k≥0,
2(k-1)=24-8k≥0,
解得:k≤3,
∵k为大于2的正整数,
∴k=3.
∴抛物线的解析式为:y=2x2+4x+2,
其对称轴为:x=﹣![]() =﹣1;
=﹣1;
(2)将抛物线y=2x2+4x+2在直线y=2上方的部分沿直线y=2翻折,
得到的图象的解析式为:y=﹣2(x+1)2+4,
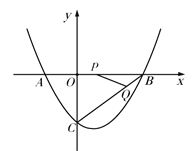
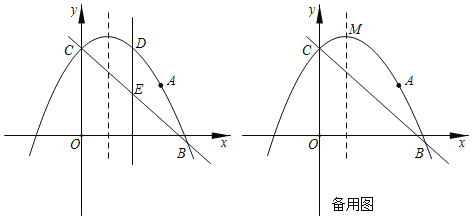
依题意可作翻折后的图象如图所示.
由图象可知,直线y=![]() x+b与新图象有两个交点,包括如下两种情况:
x+b与新图象有两个交点,包括如下两种情况:
①应使直线在点(﹣1,0)的下方,当直线y=![]() x+b经过点A(﹣1,0)时,
x+b经过点A(﹣1,0)时,
可得b=![]() ,此时b<
,此时b<![]() ,直线y=
,直线y=![]() x+b与新图象有两个交点.
x+b与新图象有两个交点.
②当直线y=![]() x+b经过点B(﹣2,2)时,
x+b经过点B(﹣2,2)时,
可得b=3;
当直线y=![]() x+b经过点C(O,2)时,可得b=2
x+b经过点C(O,2)时,可得b=2
由图象可知,符合题意的b的取值范围为:2<b<3或b<![]() .
.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目