题目内容
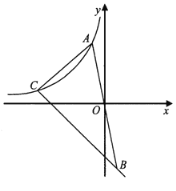
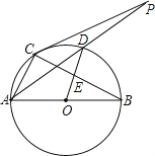
【题目】 如图,圆O是以AB为直径的△ABC的外接圆,D是劣弧![]() 的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
的中点,连AD并延长与过C点的切线交于点P,OD与BC相交于E;
(1)求证:OE=![]() AC;
AC;
(2)求证:![]() ;
;
(3)当AC=6,AB=10时,求切线PC的长.
【答案】(1)详见解析;(2)详见解析;(3)PC=15.
【解析】
(1)由于D是![]() 的中点,利用垂径定理的推论,可证OD⊥BC,而AC⊥BC,故OD∥AC,又O是AB中点,利用平行线分线段成比例定理的推论,可得BE:CE=OB:OA,从而可知E是BC中点,即OE是△ABC的中位线,利用三角形中位线定理可证OE=
的中点,利用垂径定理的推论,可证OD⊥BC,而AC⊥BC,故OD∥AC,又O是AB中点,利用平行线分线段成比例定理的推论,可得BE:CE=OB:OA,从而可知E是BC中点,即OE是△ABC的中位线,利用三角形中位线定理可证OE=![]() AC;
AC;
(2)连接CD,连接CO并延长交圆O于点F,连接DF,先证明∠PCD=∠CAP,再利用两组角对应相等,证明△PCD∽△PAC,得出![]() ,结合CD=BD利用等式性质可证;
,结合CD=BD利用等式性质可证;
(3)连接BD,由AC=6,AB=10,利用勾股定理可求BC,进而求出BE、OE、DE,再利用勾股定理可求BD2、AD2,从而解出AD、BD、CD,结合(2)中的结论,利用比例性质,可求出DP、AP,那么可求CP2,从而求出CP.
(1)证明:∵AB为直径,
∴∠ACB=90°,
∴AC⊥BC,
又D为![]() 中点,
中点,
∴OD⊥BC,OD∥AC,
又O为AB中点,
∴E为BC的中点,即OE为△ABC的中位线,
∴![]() ;
;
(2)证明:连接CD,
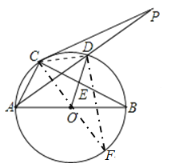
连接CO并延长交圆O于点F,连接DF,
∵PC为切线,
∴∠PCD+∠DCO==90°,∠DCO+∠F=90°,
∴∠PCD=∠F,又∠F=∠CAP,
∴∠PCD=∠CAP,
又∠P为公共角,
∴△PCD∽△PAC,
∴![]() ,
,
∴![]()
又CD=BD,
∴![]() ;
;
(3)解:连接BD,∵AC=6,AB=10,

∴BC=8,BE=4,OE=3,
∴DE=2,
∴BD2=DE2+BE2=20,∴BD=2![]() ,
,
∴AD2=AB2-BD2=80,∴AD=4![]() ,
,
∴AD=4![]() ,
,
又D为![]() 中点,∴CD=BD=2
中点,∴CD=BD=2![]() ,
,
由(2)![]() ,
,
∴![]() ,
,
由(1)中△PCD∽△PAC得,
∴CP2=DPAP=![]() ,
,
∴PC=15.