题目内容
【题目】如图,在平面直角坐标系中,正方形![]() 的边长为
的边长为![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 在坐标轴上,把正方形
在坐标轴上,把正方形![]() 绕点
绕点![]() 顺时针旋转后得到正方形
顺时针旋转后得到正方形![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,且点
,且点![]() 恰为
恰为![]() 的中点,则点
的中点,则点![]() 的坐标为________.
的坐标为________.

【答案】![]()
【解析】
根据旋转的知识可知:四边形M′N′E′O为正方形,可得OE′=N′E′,∠OE′N′=90°,∠E′OF=∠MOM′,由于F是N′E′的中点,故E′F=![]() E′N′=
E′N′=![]() OE′,由此在Rt△E′OF中,tan∠E′OF=
OE′,由此在Rt△E′OF中,tan∠E′OF=![]() ,根据三角函数与勾股定理即可求得点M′的坐标.
,根据三角函数与勾股定理即可求得点M′的坐标.
∵四边形M′N′E′O为正方形,
∴OE′=N′E′,∠OE′N′=90°.
又∵F是N′E′的中点,
∴E′F=![]() E′N′=
E′N′=![]() OE′.
OE′.
∵由旋转性质可知,∠E′OF=∠MOM′,
∴在Rt△E′OF中,tan∠E′OF=![]() ;
;
过点M′作M′G⊥x轴,垂足为点G,
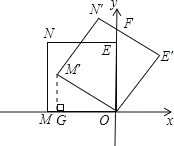
在Rt△M′GO中,tan∠MOM′=![]() ,
,
设M′G=k,则OG=2k,在Rt△M′GO中,OM′=![]() ,
,
根据勾股定理,得M′G2+OG2=OM′2.
即k2+(2k)2=(![]() )2,
)2,
解得k1=1(舍),k2=1.
∴M′G=1,OG=2.
又∵点M′在第二象限,
∴点M′的坐标为(2,1).
故答案为:(2,1).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目