题目内容
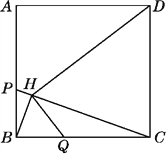
【题目】如图,P、Q分别是正方形ABCD的边AB、BC上的点,且BP=BQ,过点B作PC的垂线,垂足为点H,连接HD、HQ. (14分)
(1)图中有________对相似三角形;
(2)若正方形ABCD的边长为1,P为AB的三等分点,求△BHQ的面积;
(3)求证:DH⊥HQ.

【答案】(1)4;(2)![]() ()证明见解析.
()证明见解析.
【解析】试题分析:(1)、根据角度之间的关系得出相似三角形;(2)、过点H作HE⊥BC于点E,根据P为三等分点得出BP=BQ=![]() ,根据Rt△PBC的勾股定理以及相似三角形求出BH的长度,根据Rt△BHC的勾股定理以及三角形相似求出HE的长度,从而得出△BHQ的面积;(3)、根据Rt△PBC∽Rt△BHC得出∠HBQ=∠HCD,从而的得出△HBQ∽△HCD,即∠BHQ=∠DHC,最后根据∠BHQ+∠QHC=90°,∠QHC+∠DHC=∠QHD=90°得出垂直.
,根据Rt△PBC的勾股定理以及相似三角形求出BH的长度,根据Rt△BHC的勾股定理以及三角形相似求出HE的长度,从而得出△BHQ的面积;(3)、根据Rt△PBC∽Rt△BHC得出∠HBQ=∠HCD,从而的得出△HBQ∽△HCD,即∠BHQ=∠DHC,最后根据∠BHQ+∠QHC=90°,∠QHC+∠DHC=∠QHD=90°得出垂直.
试题解析:(1)、解:4;
(2)、解:过点H作HE⊥BC于点E, ∵正方形ABCD的边长为1,P为AB的三等分点,
 ∴BP=BQ=
∴BP=BQ=![]() .
.
在Rt△PBC中,由勾股定理得PC=![]() , ∵BP·BC=BH·PC,∴BH=
, ∵BP·BC=BH·PC,∴BH=![]() =
=![]() ,
,
在Rt△BHC中,由勾股定理得CH=![]() , ∵BH·CH=HE·BC,∴HE=
, ∵BH·CH=HE·BC,∴HE=![]() =
=![]() ,
,
∴△BHQ的面积为![]() EH·BQ=
EH·BQ=![]() ×
×![]() ×
×![]() =
=![]() ;
;
(3)、证明:∵∠PBC=∠CHB=90°,∠BCH=∠PCB,
∴Rt△PBC∽Rt△BHC,∴![]() =
=![]() , 又∵BP=BQ,BC=DC,∴
, 又∵BP=BQ,BC=DC,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,
,
∵∠BHC=∠BCD=90°,∠BCH=∠BCH,∴∠HBQ=∠HCD,
在△HBQ与△HCD中,∵![]() =
=![]() ,∠HBQ=∠HCD, ∴△HBQ∽△HCD,∴∠BHQ=∠DHC, ∴∠BHQ+∠QHC=∠DHC+∠QHC,
,∠HBQ=∠HCD, ∴△HBQ∽△HCD,∴∠BHQ=∠DHC, ∴∠BHQ+∠QHC=∠DHC+∠QHC,
又∵∠BHQ+∠QHC=90°, ∴∠QHC+∠DHC=∠QHD=90°,即DH⊥HQ.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
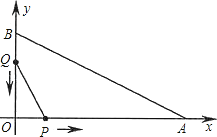
小学生10分钟应用题系列答案【题目】小东根据学习一次函数的经验,对函数y=|2x﹣1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=|2x﹣1|的自变量x的取值范围是 ;
(2)已知:
①当x=![]() 时,y=|2x﹣1|=0;
时,y=|2x﹣1|=0;
②当x>![]() 时,y=|2x﹣1|=2x﹣1
时,y=|2x﹣1|=2x﹣1
③当x<![]() 时,y=|2x﹣1|=1﹣2x;
时,y=|2x﹣1|=1﹣2x;
显然,②和③均为某个一次函数的一部分.
(3)由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m= ;n= ;:
x | … | ﹣2 | 0 |
| 1 | m | … |
y | … | 5 | 1 | 0 | 1 | n | … |
(4)在平面直角坐标系xOy中,作出函数y=|2x﹣1|的图象;
(5)根据函数的图象,写出函数y=|2x﹣1|的一条性质.

【题目】某公司有A、B两种型号的客车共11辆,它们的载客量(不含司机)、日租金、车辆数如下表所示,已知这11辆客车满载时可搭载乘客350人.
A型客车 | B型客车 | |
载客量(人/辆) | 40 | 25 |
日租金(元/辆) | 320 | 200 |
车辆数(辆) | a | b |
(1)求a、b的值;
(2)某校七年级师生周日集体参加社会实践,计划租用A、B两种型号的客车共6辆,且租车总费用不超过1700元.
①最多能租用A型客车多少辆?
②若七年级师生共195人,写出所有的租车方案,并确定最省钱的租车方案.