题目内容
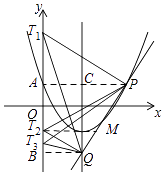
【题目】如图,抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7)且与直线y=kx﹣2k﹣3相交于点P(m,2m﹣7). 
(1)求抛物线的解析式;
(2)求直线y=kx﹣2k﹣3与抛物线y=ax2﹣(2a+1)x+b的对称轴的交点Q的坐标;
(3)在y轴上是否存在点T,使△PQT的一边中线等于该边的一半?若存在,求出点T的坐标;若不存在请说明理由.
【答案】
(1)解:∵抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7),
∴ ![]() ,
,
解得 ![]() ,
,
∴抛物线的解析式为y= ![]() x2﹣2x+1
x2﹣2x+1
(2)解:∵抛物线的图象经过点P(m,2m﹣7),
∴2m﹣7= ![]() m2﹣2m+1,
m2﹣2m+1,
解得m1=m2=4,
∴点P的坐标为(4,1),
∵直线y=kx﹣2k﹣3经过点P,
∴4k﹣2k﹣3=1,
解得k=2,
∴直线的解析式为y=2x﹣7,
∵y= ![]() x2﹣2x+1=
x2﹣2x+1= ![]() (x﹣2)2﹣1,
(x﹣2)2﹣1,
∴抛物线的对称轴为直线x=2,
∴在y=2x﹣7中,当x=2时,y=2×2﹣7=﹣3,
∴点Q的坐标为(2,﹣3)
(3)解:设点T的坐标为(0,t),M为PQ的中点,连结TM,根据题意得:
TM= ![]() PQ,即TM=PM=QM,
PQ,即TM=PM=QM,
∴点T在以PQ为直径的圆上,
∴∠PTQ=90°,
∴△PQT为直角三角形,
同理,点M为PT或QT的中点时,△PQT仍为直角三角形,
作PA⊥y轴于A,交直线x=2于点C,QB⊥y轴于B,则AT=|1﹣t|,BT=|﹣3﹣t|,
∵PA=4,QB=2,PC=2,CQ=4,
∴PQ= ![]() =
= ![]() =2
=2 ![]() ,
,
①当∠PTQ=90°时,
∵PQ2=TQ2+TP2=BT2+QB2+PA2+AT2
=|﹣3﹣t|2+22+|1﹣t|2+42=20,
∴2t2+4t+10=0,即(t+1)2=﹣4,
∵(t+1)2≥0,
∴此方程无解;
②当∠PQT=90°时,PQ2+QT2=PT2,
∴(2 ![]() )2+22+|﹣3﹣t|2=42+|1﹣t|2,
)2+22+|﹣3﹣t|2=42+|1﹣t|2,
解得t=﹣2;
③当∠QPT=90°时,TQ2=PT2+PQ2,
∴QB2+BT2=PA2+AT2+(2 ![]() )2,
)2,
∴4+|﹣3﹣t|2=16+|1﹣t|2+20,
解得t=3,
综上所述,在y轴上存在点T,其坐标分别为(0,3)和(0,﹣2),使△PQT的一边中线等于该边的一半.
【解析】(1)根据抛物线y=ax2﹣(2a+1)x+b的图象经过(2,﹣1)和(﹣2,7),求得a,b的值即可得到抛物线的解析式;(2)先根据抛物线的图象经过点P(m,2m﹣7),求得点P的坐标,再根据直线y=kx﹣2k﹣3经过点P,求得k的值,最后根据抛物线的对称轴为直线x=2,求得点Q的坐标;(3)设点T的坐标为(0,t),M为PQ的中点,连结TM,分三种情况讨论:∠PTQ=90°时,∠PQT=90°时,∠QPT=90°时,分别根据勾股定理列出关于t的方程进行求解即可.

【题目】唐山质量监督局从某食品厂生产的袋装食品中抽出样品20袋,检测每袋的质量是否符合标准,把超过或不足的部分分别用正、负数来表示,记录如下表:
与标准质量的差值(单位:克) | ﹣6 | ﹣2 | 0 | 1 | 3 | 4 |
袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
(1)若每袋食品的标准质量为450克,则抽样检测的20袋食品的总质量是多少克?
(2)若该种食品的合格标准为450±5克,求该种食品抽样检测的合格率?