题目内容
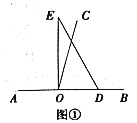
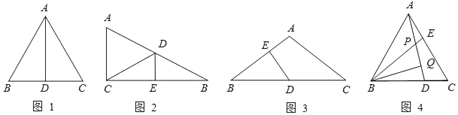
【题目】如图1所示,等边△ABC中,AD是BC边上的中线,根据等腰三角形的“三线合一”特性,AD平分∠BAC,且AD⊥BC,则有∠BAD=30°,BD=CD=![]() AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
AB.于是可得出结论“直角三角形中,30°角所对的直角边等于斜边的一半”.
请根据从上面材料中所得到的信息解答下列问题:
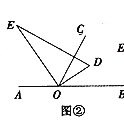
(1)如图2所示,在△ABC中,∠ACB=90°,BC的垂直平分线交AB于点D,垂足为E,当BD=5cm,∠B=30°时,求△ACD的周长.
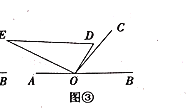
(2)如图3所示,在△ABC中,AB=AC,∠A=120°,D是BC的中点,DE⊥AB,垂足为E,求BE:EA的值.
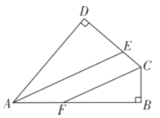
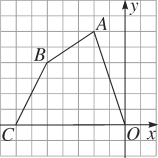
(3)如图4所示,在等边△ABC中,D、E分别是BC、AC上的点,且AE=DC,AD、BE交于点P,作BQ⊥AD于Q,若BP=2,求PQ的长.
【答案】(1)15cm;(2)3:1;(3)PQ=1.
【解析】
(1)根据线段垂直平分线的性质知CD=BD,得出△ACD的周长=AC+AB;
(2)连接AD.利用等腰三角形的性质、垂直的定义推知∠B=∠ADE=30°,然后由”30度角所对的直角边是斜边的一半“分别求得BE、AE的值,即可得出结果;
(3)根据全等三角形的判定定理SAS证明△BAE≌△ACD,根据全等三角形的对应角相等,以及三角形外角的性质,可以得到∠PBQ=30°,根据直角三角形的性质得出PQ=1,再由勾股定理求出BQ即可.
解:(1)∵DE是线段BC的垂直平分线,∠ACB=90°,
∴CD=BD,AD=BD.
又∵在△ABC中,∠ACB=90°,∠B=30°,
∴![]()
∴△ACD的周长=AC+AB=3BD=15cm.
故答案为:15cm;
(2)如图,连接AD,
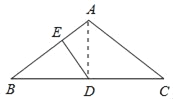
∵在△ABC中,AB=AC,∠A=120°,D是BC的中点,
∴∠BAD=60°.
又∵DE⊥AB,
∴∠B=∠ADE=30°,
∴![]()
∴![]()
又∵![]()
∴BE:AE=3:1.
故答案为:3:1.
(3)∵△ABC为等边三角形.
∴AB=AC,∠BAC=∠ACB=60°,
在△BAE和△ACD中,
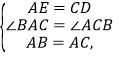
∴△BAE≌△ACD(SAS),
∴∠ABE=∠CAD.
∵∠BPQ为△ABP外角,
∴∠BPQ=∠ABE+∠BAD.
∴∠BPQ=∠CAD+∠BAD=∠BAC=60°
∵BQ⊥AD,
∴∠PBQ=30°,
∴BP=2PQ=2,
∴PQ=1.