题目内容
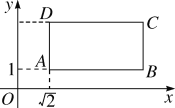
【题目】如图,有一块不规则的四边形地皮ABCO,各个顶点的坐标分别为A(-2,6),B(-5,4),C(-7,0),O(0,0)(图上一个单位长度表示10米),现在想对这块地皮进行规划,需要确定它的面积.
(1)求这个四边形的面积;
(2)如果把四边形ABCD的各个顶点的纵坐标保持不变,横坐标加2,所得到的四边形面积是多少?
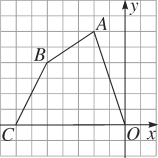
【答案】(1) 2500平方米;(2)所得到的四边形的面积与原四边形的面积相等,为2500平方米.
【解析】
(1)过点A作AG⊥x轴于点G,过点B作BF⊥x轴于点F,把四边形ABCO的面积分成两个三角形的面积与梯形的面积的和,然后列式求解即可;
(2)横坐标增加2,纵坐标不变,就是把四边形ABCO向右平移2个单位,根据平移的性质,四边形的面积不变.
(1)过B作BF⊥x轴于F,过A作AG⊥x轴于G,如图所示.
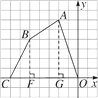
∴S四边形ABCO=S三角形BCF+S梯形ABFG+S三角形AGO
=[![]() ]
]
×102=2500(平方米).
(2)把四边形ABCO的各个顶点的纵坐标保持不变,横坐标加2,即将这个四边形向右平移2个单位长度,
故所得到的四边形的面积与原四边形的面积相等,为2500平方米.

练习册系列答案
相关题目