Question

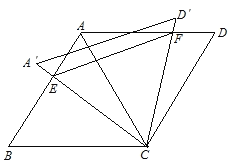
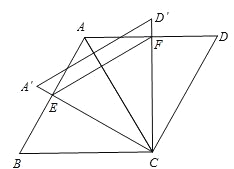
【题目】如图,菱形ABCD中,边长为2,∠B=60°,将△ACD绕点C旋转，当AC（即A′C）与AB交于一点E,CD（即CD′）同时与AD交于一点F时,点E，F和点A构成△AEF。试探究△AEF的周长是否存在最小值,如果不存在，请说明理由；如果存在,请计算出△AEF周长的最小值.

Answer 1

【答案】2+

【解析】试题分析：根据菱形和旋转的性质，以及∠B=60°，可得△ABC，△ACD和△A′CD′是等边三角形，推出∠BCE=∠ACF，证出△BCE≌△ACF（ASA），得出BE=AF，CE=CF，推出△ECF是等边三角形，根据CF的最小值为点C到AD的距离，即EF的最小值是，可求出△AEF的周长的最小值.

试题解析：△AEF的周长存在最小值。理由如下：

根据菱形和旋转的性质，以及∠B=60°，可得△ABC，△ACD和△A′CD′是等边三角形，

∴∠BCA=∠BCE+∠ACE=60°，∠ECF=∠ACF+∠ACE=60°。

∴∠BCE=∠ACF

在△BCE与△ACF中，

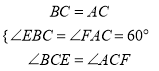
∴△BCE≌△ACF（ASA）

∴BE=AF，CE=CF，AE+AF=AE+BE=AB，

∵∠ECF=60°，

故△ECF是等边三角形，

EF=CF

∵CF的最小值为点C到AD的距离（如图），

∴EF的最小值是。

∵△AEF的周长=AE+AF+EF=AB+EF，

∴△AEF的周长的最小值为2+。