题目内容
【题目】已知:如图,ABCD中,对角线AC、BD交于点O,直线EF经过点O,分别交DA,BC的延长线于点E,F,连接BE,DF. 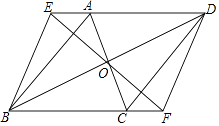
求证:
(1)AE=CF;
(2)四边形BEDF是平行四边形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC,
∴∠AEO=∠CFO,
∵∠AOE=∠COF,
∴△AOE≌△COF,
∴AE=CF

(2)证明:∵四边形ABCD是平行四边形,
∴AD=BC,
∵AE=CF,
∴AD+AE=BC+CF,
∴DE=BF,
∵DE∥BF,
∴四边形BEDF是平行四边形.
【解析】(1)只要证明△AOE≌△COF即可;(2)只要证明DE=BF,DE∥BF即可;
【考点精析】本题主要考查了平行四边形的判定与性质的相关知识点,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目