Question

已知：如图，在四边形ABCD中，∠BAD=150°，∠D=90°，AD=2，AB=5，CD=2

3

．求四边形ABCD的周长．

Answer 1

分析：连接AC，利用勾股定理求出AC的长，再利用锐角三角函数求出角DAC的度数，再由已知条件求出∠BAC的度数为90°，利用勾股定理即可求出BC的长，问题得解．

解答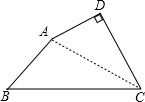：解：连接AC
在Rt△ADC中，
∵∠D=90°，AD=2，CD=2

3

，
∴AC=

AD2+CD2

=4，
∵AD=2，
∴∠DCA=30°，∠DAC=60°，
∵∠BAD=150°，
∴∠BAC=90°，
∴BC=

AC2+AB2

=

41

，
四边形ABCD的周长为：7+2

3

+

41

．

点评：本题考查了勾股定理和锐角三角函数的运用，注意求不规则图形的周长可以转化为求一些规则图形的周长的和或差的问题．