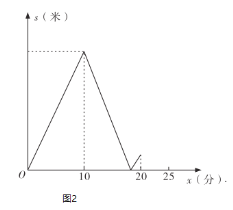
题目内容
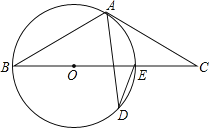
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于点E,连接CE.
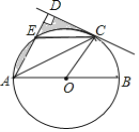
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是弧AC的中点,⊙O的半径为2,求图中阴影部分的面积.
【答案】(1)CD与圆O相切,证明见解析;(2)![]() ;
;
【解析】
(1)只要证明OC∥AD即可解决问题.
(2)只要证明四边形AECO是菱形,∠DEC=∠DAO=60°,根据S阴影=S△DEC即可解决问题.
(1)CD与圆O相切,理由如下:
∵AC为∠DAB的平分线,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
则CD与圆O相切;
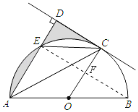
(2)连接EB,交OC于F,
∵AB为直径,
∴∠AEB=90°,
∴EB∥CD,
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∴∠EAC=∠ACO,
∵弧AE=弧EC,
∴AE=EC,
∴∠EAC=∠ECA,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠ECA=∠OAC,
∴EC∥OA,
∴四边形AECO是平行四边形,
∵OA=OC,
∴四边形AECO是菱形,
∴AE=EC=OA=OC=2,易知∠DEC=∠DAO=60°,
∴DE=![]() EC=1,DC=
EC=1,DC=![]() DE=
DE=![]()
∵点O为AB的中点,∴OF为ΔABE的中位线,
∴OF=![]() AE=1,即CF=DE=1,在RtΔOBF中,根据勾股定理得:EF=FB=DC=
AE=1,即CF=DE=1,在RtΔOBF中,根据勾股定理得:EF=FB=DC=![]() ,
,
则![]() .
.

练习册系列答案
相关题目