Question

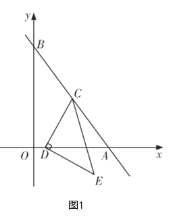
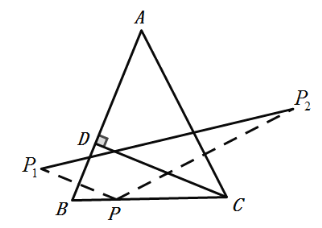
【题目】如图，在三角形中，，，为边上的高，，点为边上的一动点，，分别为点关于直线，的对称点，连接，则线段长度的取值范围是__________.

Answer 1

【答案】8.

【解析】

连接AP1、AP2、AP，过点A作AE⊥于点E，由对称性可知AP1=AP= AP2、△P1AP2是等腰直角三角形，进而即可得出=AP，再根据AP的取值范围即可得出线段长的取值范围．

连接AP1、AP2、AP，过点A作AE⊥于点E，如图所示。

∵点P关于直线AB，AC的对称点分别为，，

∴AP1=AP= AP2，∠AB=∠PAB，∠AC=∠PAC，

∵

∴△P1AP2等腰直角三角形，

∴∠AE=45，

∴AE=E=A,=AP，

∵，为边上的高，，，

∴AD=CD=6,BD=2,/span>

∴BC=

作AP’⊥BC，

∴BP’=

∴AP’=

∴AP’APAB，

即AP8

∵=AP，

∴8.

故答案为：8.