题目内容
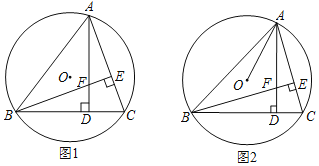
【题目】如图,等腰△ABC中,底边BC长为8,腰长为6,点D是BC边上一点,过点B作AC的平行线与过A、B、D三点的圆交于点E,连接DE,则DE的最小值是___.

【答案】2![]() .
.
【解析】
如图,连接AE,AD,OE,OD,作AJ⊥BC于J,OK⊥DE于K.首先证明∠EOD=2∠C=定值,推出⊙O的半径最小时,DE的值最小,推出当AB是直径时,DE的值最小.
如图,连接AE,AD,OE,OD,作AJ⊥BC于J,OK⊥DE于K.
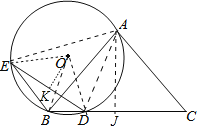
∵BE∥AC,
∴∠EBC+∠C=180°,
∵∠EBC+∠EAD=180°,
∴∠EAD=∠C,
∵∠EOD=2∠EAD,
∴∠EOD=2∠C=定值,
∴⊙O的半径最小时,DE的值最小,
∴当AB是⊙O的直径时,DE的值最小,
∵AB=AC=6,AJ⊥BC,
∴BJ=CJ=4,
∴AJ=![]() =
=![]() =2
=2![]() ,
,
∵OK⊥DE,
∴EK=DK,
∵AB=6,
∴OE=OD=3,
∵∠EOK=∠DOK=∠C,
∴sin∠EOK=sin∠C=![]() ,
,
∴![]() =
=![]() ,
,
∴EK=![]() ,
,
∴DE=2![]() ,
,
∴DE的最小值为2![]() .
.
故答案为2![]() .
.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目