题目内容
【题目】阅读下列材料，完成任务：
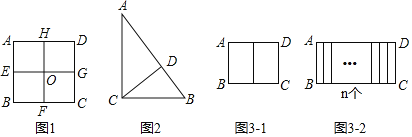
自相似图形，定义：若某个图形可分割为若干个都与它相似的图形，则称这个图形是自相似图形．例如：正方形ABCD中，点E、F、G、H分别是AB、BC、CD、DA边的中点，连接EG，HF交于点O，易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形，且与原正方形相似，故正方形是自相似图形．
（1）图1中正方形ABCD分割成的四个小正方形中，每个正方形与原正方形的相似比为______；
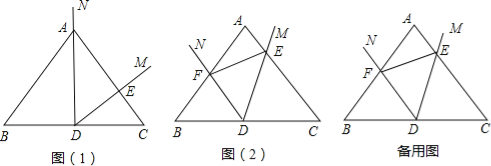
（2）如图2，已知△ABC中，∠ACB＝90°，AC＝4，BC＝3，小明发现△ABC也是“自相似图形”，他的思路是：过点C作CD⊥AB于点D，则CD将△ABC分割成2个与它自己相似的小直角三角形．则△ACD与△ABC的相似比为_____；则△BCD与△ABC的相似比为_____；
（3）现有一个矩形ABCD是自相似图形，其中长AD＝a，宽AB＝b（a＞b）．
①如图3﹣1，若将矩形ABCD纵向分割成两个全等矩形，且与原矩形都相似，则a＝_____（用含b的式子表示）：
②如图3﹣2，若将矩形ABCD纵向分割成n个全等矩形，且与原矩形都相似，则a＝______（用含n，b的式子表示）．
【答案】（1）
；（2）
，
；（3）①
b；②
b．
【解析】
（1）先得出AH＝AD，然后进一步即可得出结论；
（2）根据勾股定理求出AB，然后通过相似三角形性质进一步求解即可得出结论；
（3）①根据矩形ABEF∽矩形FECD得出比例式即可得出结论；②同①的方法即可得出结论；
（1）∵点H是AD的中点，
∴AH＝AD，
∵正方形AEOH∽正方形ABCD，
∴相似比为：
；
故答案为：；
（2）在Rt△ABC中，AC＝4，BC＝3，根据勾股定理得，AB＝5，
∴△ACD与△ABC相似的相似比为：
，△BCD与△ABC的相似比为：
，
故答案为：，；
（3）①∵矩形ABEF∽矩形FECD，
∴AF：AB＝AB：AD，
即a：b＝b：a，
∴a＝b；
故答案为：b
②每个小矩形都是全等的，则其边长为b和
a，
则b：a＝a：b，
∴a＝b；
故答案为：b
