Question

【题目】已知锐角三角形ABC内接于⊙O（AB＞AC），AD⊥BC于点D，BE⊥AC于点E，AD、AE交于点F．

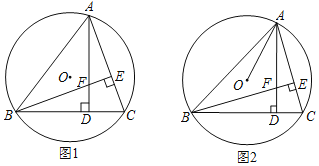
（1）如图1，若⊙O直径为10，AC＝8，求BF的长；

（2）如图2，连接OA，若OA＝FA，AC＝BF，求∠OAD的大小．

Answer 1

【答案】（1）BF＝6；（2）∠OAD＝30°．

【解析】

（1）如图1中，作⊙O的直径CM，连接AM，BM．利用勾股定理求出AM，证明四边形AMBF是平行四边形即可解决问题；
（2）如图2中，作⊙O的直径CM，连接AM，BM，设AD交CM于J．证明AO⊥CM．推出∠OAD＝∠BCM，解直角三角形求出∠BCM即可解决问题．

（1）如图1中，作⊙O的直径CM，连接AM，BM．

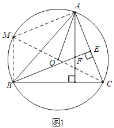
∵CM是直径，

∴∠CAM＝∠CBM＝90°，

∵CM＝10，AC＝8，

∴AM＝＝＝6，

∵AD⊥CB，BE⊥AC，

∴∠ADC＝∠MBC＝90°，∠BEC＝∠MAC＝90°，

∴AD∥BM，AM∥BE，

∴四边形AMBF是平行四边形，

∴BF＝AM＝6．

（2）如图2中，作⊙O的直径CM，连接AM，BM，设AD交CM于J．

由（1）可知四边形AMBF是平行四边形，

∴AM＝BF，AF＝BM

∵AC＝BF，

∴AC＝AM，

∵∠MAC＝90°，MO＝OC，

∴AO⊥CM，

∵AD⊥BC，

∴∠AOJ＝∠CDJ＝90°，

∵∠AJO＝∠CJD，

∴∠DCJ＝∠JAO，

∵AF＝OA，AF＝BM，

∴OA＝BM，

∴CM＝2BM，

∵∠CBM＝90°，

∴sin∠BCM＝＝，

∴∠BCM＝30°，

∴∠OAD＝∠BCM＝30°．