��Ŀ����
����Ŀ�������龳
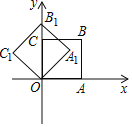
��ͼ 1����ABC �У��ء�BAC ��ƽ���� AB1 �۵��������ص����֣������²����ء�B1A1C ��ƽ���� A1B2 �� ���������ص����֣���˷����������� ��Bn An C ��ƽ���� An Bn��1 �۵����� Bn ��� C �غϣ����Ǿͳ� ��BAC�ǡ�ABC �����ǣ�
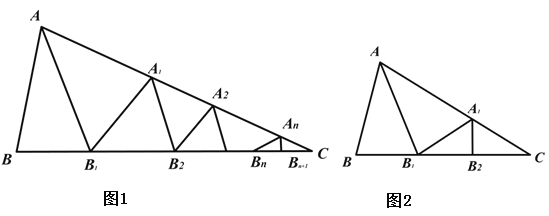
��ͼ 2 Ϊ������ABC �У���B=70�㣬��C=35�㣬���ء�BAC ��ƽ���� AB1 �۵������AA1B=70��.�� A1B1 �����ص����֣������µġ�B1A1C �У��������ε��ڽǺͶ�����֪��A1B1C=35�㣬���ء�B1A1C ��ƽ���� A1B2 �ڶ����۵������ B1 ��� C �غ�. ��ʱ�����Ǿͳơ�BAC �ǡ�ABC ������.
̽������
��1����ABC �У���B= 2��C ���������۵���BAC �Dz��ǡ�ABC �����ǣ� ����ǡ����ǡ� ) .
��2��С�����������۵����֡�BAC �ǡ�ABC �����ǣ��� ��B ���C �������� ��B ����C ) ֮��ĵ�����ϵ Ϊ ��
�����������ݲ��룺������ n ���۵� ��BAC �ǡ�ABC �����ǣ����B �� ��C ���������B�� ��C ) ֮�� �ĵ�����ϵΪ ��
Ӧ������
��3�����һ�������ε���С���� 10�㣬ֱ��д�������������������ǵĶ�����ʹ�ô������ε������Ǿ��� ��������.
���𰸡���1���ǣ���2�� B 3C �� B nC����3��10����160��
��������
��1����ϸ������������۵������ʼ����С����ǡ��Ķ��弴�������жϣ�
��2����Ϊ���������۵���BAC�ǡ�ABC�����ǣ����Ե������۵��ġ�A2 B2C=��C���ɡ�AB B1=��AA1B1����AA1B1=��A1B1C+��C���֡�A1B1C=��A1A2B2����A1A2B2=��A2B2C+��C����ABB1=��A1B1C+��C=��A2B2C+��C+��C=3��C���ɴ˼�����ý����
��3����Ϊ��С����10���ǡ�ABC�����ǣ��������Ƕ��壬����������Ƿֱ�Ϊ10m�㣬10mn�㣨����m��n���������������������10m+10mn+10=180������m��n+1��=17���ٸ���m��n�����������ɵ�m��n+1��17���������ӣ��Ӷ�������ý��.
��1�����ء�BAC��ƽ����AB1�۵���
���B=��AA1B1��
�֡ߡ�AA1B1=��A1B1C+��C�ҡ�B= 2��C
��2��C=��A1B1C+��C����C=��A1B1C
����ƽ����A1B2
���B1 A1 B2 =��C A1 B2
�� B1 A1 B2�� C A1 B2
�ཫ���²����ء�B1A1C��ƽ����A1B2�۵�����ʱ��B1���C�غϣ�
���BAC�Dz��ǡ�ABC������
����ǣ�
��2���۵����������ͼ��

�߸����۵�������֪����B=��AA1B1����A1B1C=��A1A2B2����C=��A2B2C��
���A1A2B2=��C+��A2B2C=2��C��
���AA1B1=��A1B1C+��C=��A1A2B2+��C=2��C+��C=3��C
���B=��AA1B1=3��C������B=3��C
�����B=3��C��
���۵�1��֪������B=��Cʱ����BAC�ǡ�ABC�����ǣ�
���۵�2��֪������B=2��Cʱ����BAC�ǡ�ABC�����ǣ�
���۵�3��֪������B=3��Cʱ����BAC�ǡ�ABC�����ǣ�
��������n���۵���BAC�ǡ�ABC������,���B���C(�������B>��C)֮��ĵ�����ϵΪ��B=n��C
�����B=n��C��
��3���ɡ�B=n��C����BAC�ǡ�ABC�����ǣ�
��Ϊ��С����10���ǡ�ABC�����ǣ�
�������Ƕ���,����������Ƿֱ�Ϊ10m��,10mn��(����m��n����������)��
������,��10m+10mn+10=180,����m(n+1)=,17��
��m��n����������������m��n+1��17���������ӣ�
��m=1��n+1=17��
��m=1��n=16��
��10m=10��,10mn=160����
��������ε����������ǵĶ����ֱ�Ϊ��10����160��.

 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д� �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�