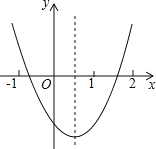题目内容
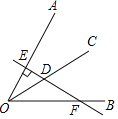
【题目】对于任意一点 P 和线段 a.若过点 P 向线段 a 所在直线作垂线,若垂足落在线段 a 上,则称点 P 为线段a 的内垂点.在平面直角坐标系 xOy 中,已知点 A(-1,0),B(2,0 ) ,C(0,2).
(1)在点 M(1,0),N(3,2),P(-1,-3)中,是线段 AB 的内垂点的是 ;
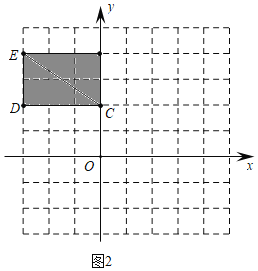
(2)已知点 D(-3,2),E(-3,4).在图中画出区域并用阴影表示,使区域内的每个点均为 Rt△CDE三边的内垂点;
(3)已知直线 m 与 x 轴交于点 B,与 y 轴交于点 C,将直线 m 沿 y 轴平移 3 个单位长度得到直线 n . 若存在点 Q,使线段 BQ 的内垂点形成的区域恰好是直线 m 和 n 之间的区域(包括边界),直接写出点 Q 的坐标.
【答案】(1)M,P;(2)见详解;(3)(0.5,﹣1.5)或(3.5,1.5)
【解析】
(1)画图后根据定义可以判定;
(2)如图2所示;
(3)分两种情况:①n在m的下方,②n在m的上方,先确认m和n的解析式,n与x轴的交点为E,作BE的垂直平分线,与n的交点即是Q.
解:(1)如图1所示:PA⊥AB,垂足为A,过M作AB的垂线,垂足为M,都在线段AB上,
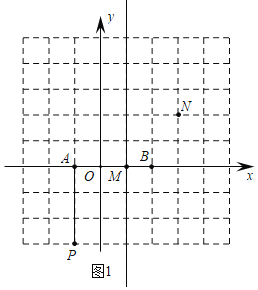
所以线段AB的内垂点的是:M,P;
故答案为:M,P;
(2)如图2所示,
(3)分两种情况:
①当n在m的下方时,如图3,

∵B(2,0),C(0,2).
设BC的解析式为:y=kx+b,则![]() ,
,
解得:![]() ,
,
∴m:y=﹣x+2,
n:y=﹣x﹣1,
∴E(﹣1,0),
取BE的中点P,过P作BE的垂线交n于Q,
∵P(0.5,0),
∴当x=0.5时,y=﹣x﹣1=﹣1.5,
∴Q(0.5,﹣1.5);
②当直线n在直线m的上方时,如图4,则n:y=﹣x+5,
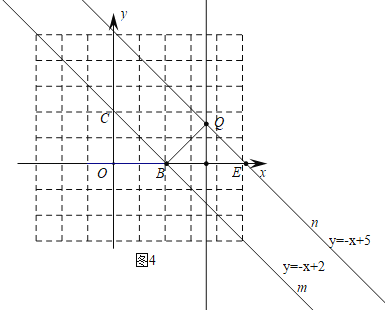
同理得Q(3.5,1.5);
综上,点Q的坐标为(0.5,﹣1.5)或(3.5,1.5).