题目内容
【题目】化简:cos21°+cos22°+cos23°+…+cos289°.
【答案】解:cos21°+cos22°+cos23°+…+cos289°
=cos21°+cos289°+…+cos244°+cos246°+cos245°
=(cos21°+cos289°)+…+(cos244°+cos246°)+( ![]() )2
)2
= ![]() +
+ ![]()
=44 ![]()
【解析】根据锐角三角函数关系式:互为余角的两个角的余弦平方和等于1.
还要注意cos45°= ![]() .
.
【考点精析】本题主要考查了互余两角的三角函数关系的相关知识点,需要掌握互余关系:sinA=cos(90°—A),cosA=sin(90°—A),tanA=cot(90°—A),cotA=tan(90°—A)才能正确解答此题.

练习册系列答案
相关题目
【题目】某学习小组在研究函数y= ![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
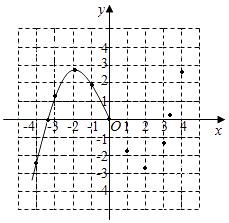
(1)请补全函数图象;
(2)方程 ![]() x3﹣2x=﹣2实数根的个数为;
x3﹣2x=﹣2实数根的个数为;
(3)观察图象,写出该函数的两条性质.



