��Ŀ����
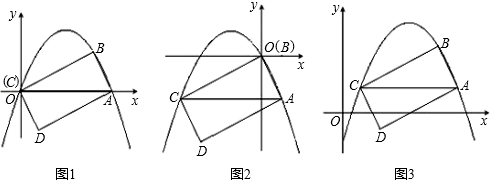
������P��y=ax2+b ��a��0��b��0����x���ཻ��A��B���㣨A��B��ࣩ����y�ύ�ڵ�C����������P����x������ԳƱ任���ٽ��任�������������ƽ��m����λ��m��0�����õ���������P1���䶥��ΪD����x���ཻ��E��F���㣨F��E��ࣩ����y���ཻ�ڵ�G��
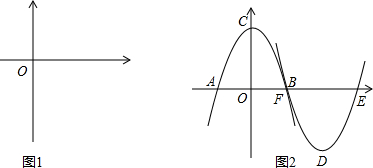
��1����a=-1��b=2����������P1��ԭ��ʱ��ֱ��д��������P1����ʽ���ڵ�D��������P��ʱ��ֱ��д��������P1�Ľ���ʽ��
��2����ͼ2����������P1����Bʱ�����ı���ADECΪ����ʱ�������a��bӦ����Ĺ�ϵʽ��
��3����a=-1��b=2ʱ������OFG�͡�OGE���ƣ���m��ֵ��
��1����a=-1��b=2����������P1��ԭ��ʱ��ֱ��д��������P1����ʽ���ڵ�D��������P��ʱ��ֱ��д��������P1�Ľ���ʽ��
��2����ͼ2����������P1����Bʱ�����ı���ADECΪ����ʱ�������a��bӦ����Ĺ�ϵʽ��
��3����a=-1��b=2ʱ������OFG�͡�OGE���ƣ���m��ֵ��
��������1����a��b��ֵ����õ�������P�Ľ���ʽ��д������x��ԳƲ�����ƽ��m����λ�������߽���ʽ���ٰ�ԭ�����������м��㼴�����������P1����ʽ��
�ڰѵ�D���������������P�Ľ���ʽ���m��ֵ���Ӷ��ý⣻
��2�����������߽���ʽ�����B��C�����꣬�Ӷ��õ�OB��OC�ij��ȣ��ٸ��ݹ��ɶ������BC�ij��ȣ�Ȼ����������ߵĶԳ����Լ����εĶԽ�����ƽ���������ʽ�������ɵõ�ab�Ĺ�ϵ��
��3��������m��ʾ��������P1����ʽ���OG�ij��ȣ��ٸ���ƽ�Ʊ�ʾ��OE��OF�ij��ȣ�Ȼ��������������ζ�Ӧ�߳ɱ�����ʽ��⼴�ɵõ�m��ֵ��
�ڰѵ�D���������������P�Ľ���ʽ���m��ֵ���Ӷ��ý⣻
��2�����������߽���ʽ�����B��C�����꣬�Ӷ��õ�OB��OC�ij��ȣ��ٸ��ݹ��ɶ������BC�ij��ȣ�Ȼ����������ߵĶԳ����Լ����εĶԽ�����ƽ���������ʽ�������ɵõ�ab�Ĺ�ϵ��
��3��������m��ʾ��������P1����ʽ���OG�ij��ȣ��ٸ���ƽ�Ʊ�ʾ��OE��OF�ij��ȣ�Ȼ��������������ζ�Ӧ�߳ɱ�����ʽ��⼴�ɵõ�m��ֵ��
����⣺��1����a=-1��b=2��
��������P��y=-x2+2��
��������P����x��Գƣ�������ƽ��m����λ�õ�������P1��
��������P1�Ľ���ʽΪy=��x-m��2-2��
��������P1��ԭ�㣬��0-m��2-2=0��
���m=
��
���ԣ�������P1����ʽΪy=��x-
��2-2��
�ڡ�������P1�Ķ���D��m��-2����������P�ϣ�
��-m2+2=-2��
���m=2��
��������P1����ʽΪy=��x-2��2-2��
��2����y=0����ax2+b=0��
���x=
��
��x=0����y=b��
���B��
��0����C��0��b����
��OB=
��OC=b��
��Rt��BOC��BC=
=
��
���ݶԳ��Կɵ�AB=BE��CB=BD����C��B��D��ͬһֱ���ϣ�
���ı���ADECΪƽ���ı��Σ�
Ҫʹ�ı���ADECΪ���Σ���AE=CD��
��4��
=2��
��
�����ã�-
=-
+b2��
���ԣ�ab=-3��
��3������a=-1��b=2��
��������P��y=-x2+2��
��y=0����-x2+2=0��
���x=��
��
���A��-
��0����B��
��0����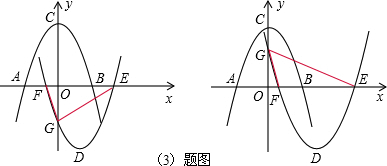
��������P����x��Գƣ�������ƽ��m����λ�õ�������P1��
��������P1�Ľ���ʽΪy=��x-m��2-2��
��E��
+m��0������F��-
+m����
��x=0����y=��0-m��2-2=m2-2��
���G��������0��m2-2����
��OE=
+m��OF=|-
+m|��OG=|m2-2|��
�ߡ�OFG�͡�OGE���ƣ�
��
=
��
��OG2=OE•OF��
�ࣨm2-2��2=��
+m��•|-
+m|=|m2-2|��
�����ã�m2-2=1��m2-2=-1��
���m=
��m=1��
��������P��y=-x2+2��
��������P����x��Գƣ�������ƽ��m����λ�õ�������P1��
��������P1�Ľ���ʽΪy=��x-m��2-2��
��������P1��ԭ�㣬��0-m��2-2=0��
���m=
| 2 |
���ԣ�������P1����ʽΪy=��x-
| 2 |
�ڡ�������P1�Ķ���D��m��-2����������P�ϣ�
��-m2+2=-2��
���m=2��
��������P1����ʽΪy=��x-2��2-2��
��2����y=0����ax2+b=0��
���x=
-
|
��x=0����y=b��
���B��
-
|
��OB=
-
|
��Rt��BOC��BC=
| OB2+OC2 |
-
|
���ݶԳ��Կɵ�AB=BE��CB=BD����C��B��D��ͬһֱ���ϣ�
���ı���ADECΪƽ���ı��Σ�
Ҫʹ�ı���ADECΪ���Σ���AE=CD��
��4��
-
|
-
|
�����ã�-
| 4b |
| a |
| b |
| a |
���ԣ�ab=-3��
��3������a=-1��b=2��
��������P��y=-x2+2��
��y=0����-x2+2=0��
���x=��
| 2 |
���A��-
| 2 |
| 2 |

��������P����x��Գƣ�������ƽ��m����λ�õ�������P1��
��������P1�Ľ���ʽΪy=��x-m��2-2��
��E��
| 2 |
| 2 |
��x=0����y=��0-m��2-2=m2-2��
���G��������0��m2-2����
��OE=
| 2 |
| 2 |
�ߡ�OFG�͡�OGE���ƣ�
��
| OE |
| OG |
| OG |
| OF |
��OG2=OE•OF��
�ࣨm2-2��2=��
| 2 |
| 2 |
�����ã�m2-2=1��m2-2=-1��
���m=
| 3 |
�����������ۺϿ����˶��κ�������Ҫ�����˹���x��Գ��Լ�ƽ�Ʊ任�������ߵĽ���ʽ��д�������εĶԽ�����ƽ������ȣ����������εĶ�Ӧ�߳ɱ��������ʣ��ܹ�д������x��ԳƲ�ƽ�ƺ��������P1�Ľ���ʽ�ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
��ͼ����ֱ֪��l��y=
x��������C��y=ax2+bx+c��a��0������������Cͼ���ϲ��ֵ�Ķ�Ӧ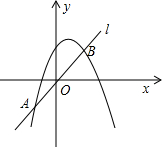 ֵ���±���
ֵ���±���
��1����������C��Ӧ�ĺ�������ʽ��
��2����ֱ��l��������C�Ľ���A��B�����ꣻ
��3��������M��ֱ��l�Ϸ���������C���ƶ������ABM�ı�AB�ϵĸ�h�����ֵ��
| 3 |
| 2 |
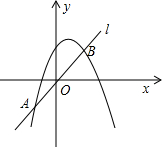 ֵ���±���
ֵ���±���| x | �� | -2 | -1 | 0 | 1 | 2 | 3 | 4 | �� |
| y | �� | -5 | 0 | 3 | 4 | 3 | 0 | -5 | �� |
��2����ֱ��l��������C�Ľ���A��B�����ꣻ
��3��������M��ֱ��l�Ϸ���������C���ƶ������ABM�ı�AB�ϵĸ�h�����ֵ��
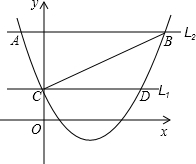
 l2����P��1��3�������ĶԳƣ�
l2����P��1��3�������ĶԳƣ�