题目内容
已知抛物线l1:y=ax2-2amx+am2+2m+1(a>0,m>0)的顶点为A,抛物线l2的顶点B在y轴上,且抛物线l1和 l2关于P(1,3)成中心对称.
l2关于P(1,3)成中心对称.(1)当a=1时,求l2的解析式和m的值;
(2)设l2与x轴正半轴的交点是C,当△ABC为等腰三角形时,求a的值.
分析:(1)首先求出顶点坐标,再代入直线解析式,分析得出二次函数解析式,利用相似△BPE∽△BAF,得出m的值;
(2)假设△ABC为等腰三角形,根据等腰三角形的性质分析得出C点的坐标,从而求出解析式.
(2)假设△ABC为等腰三角形,根据等腰三角形的性质分析得出C点的坐标,从而求出解析式.
解答: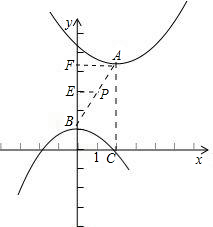 解:(1)当a=1时,∵y=ax2-2amx+am2+2m+1=(x-m)2+2m+1,
解:(1)当a=1时,∵y=ax2-2amx+am2+2m+1=(x-m)2+2m+1,
∴顶点A(m,2m+1),
又∵P(1,3),
设AB的解析式是y=kx+b,
把点A,P的坐标代入得:
①-②,得:2m-2=(m-1)k,
∵m≠1(若m=1,则A,B,P三点重合,不合题意),
∴k=2,b=1,
∴AB的解析式是y=2x+1,得l2的顶点B(0,1),
∵抛物线l1和l2关于P(1,3)成中心对称.
∴抛物线的开口大小相同,方向相反,得l2的解析式是:y=-x2+1,
∵点A,B关于点P(1,3)成中心对称,做PE⊥y轴,于点E,做AF⊥y轴于点F,则
△BPE∽△BAF,所以AF=2PE,即m=2;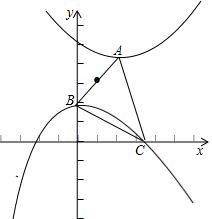
(2)在Rt△ABF中,∵AB=
=2
<5,
∴当△ABC为等腰三角形时,只有以下两种情况:
如图:若BC=AB=2
,则OC=
=
,
得C(
,0)
∵C(
,0)在y=-ax2+1上,
∴a=
.
如图:若AC=BC,设C(X,0),做AD⊥x轴于点D,在Rt△OBC中,BC2=x2+1,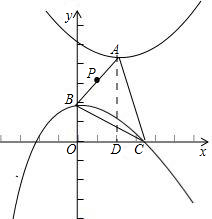
在Rt△ADC中,AC2=(x-2)2+25,由x2+1=(x-2)2+25,
解得:x=7,
∵C(7,0)在y=-ax2+1上,所以a=
,
综上所述,满足△ABC为等腰三角形a的值有两个:a=
,a=
.
 解:(1)当a=1时,∵y=ax2-2amx+am2+2m+1=(x-m)2+2m+1,
解:(1)当a=1时,∵y=ax2-2amx+am2+2m+1=(x-m)2+2m+1,∴顶点A(m,2m+1),
又∵P(1,3),
设AB的解析式是y=kx+b,
把点A,P的坐标代入得:
|
①-②,得:2m-2=(m-1)k,
∵m≠1(若m=1,则A,B,P三点重合,不合题意),
∴k=2,b=1,
∴AB的解析式是y=2x+1,得l2的顶点B(0,1),
∵抛物线l1和l2关于P(1,3)成中心对称.
∴抛物线的开口大小相同,方向相反,得l2的解析式是:y=-x2+1,
∵点A,B关于点P(1,3)成中心对称,做PE⊥y轴,于点E,做AF⊥y轴于点F,则
△BPE∽△BAF,所以AF=2PE,即m=2;

(2)在Rt△ABF中,∵AB=
| 22+42 |
| 5 |
∴当△ABC为等腰三角形时,只有以下两种情况:
如图:若BC=AB=2
| 5 |
| BC2-OB2 |
| 19 |
得C(
| 19 |
∵C(
| 19 |
∴a=
| 1 |
| 19 |
如图:若AC=BC,设C(X,0),做AD⊥x轴于点D,在Rt△OBC中,BC2=x2+1,

在Rt△ADC中,AC2=(x-2)2+25,由x2+1=(x-2)2+25,
解得:x=7,
∵C(7,0)在y=-ax2+1上,所以a=
| 1 |
| 49 |
综上所述,满足△ABC为等腰三角形a的值有两个:a=
| 1 |
| 19 |
| 1 |
| 49 |
点评:此题主要考查了中心对称的性质,以及二次函数的对称性和等腰三角形的判定,题目综合性较强,注意从已知入手细心分析.

练习册系列答案
相关题目
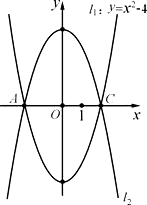 1关于x轴对称,以AC为对角线的平行四边形ABCD的第四个顶点为D.
1关于x轴对称,以AC为对角线的平行四边形ABCD的第四个顶点为D. 28、如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点,
28、如图,已知抛物线l1:y=x2-4的图象与x有交于A、C两点,