题目内容
如图,已知直线l:y=| 3 |
| 2 |
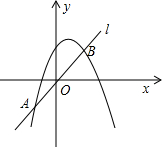 值如下表:
值如下表:| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -5 | 0 | 3 | 4 | 3 | 0 | -5 | … |
(2)求直线l与抛物线C的交点A、B的坐标;
(3)若动点M在直线l上方的抛物线C上移动,求△ABM的边AB上的高h的最大值.
分析:(1)可任选三点坐标代入抛物线的解析式中进行求解即可.(可选其中与x轴的交点,用交点式二次函数通式设抛物线的解析式求解.)
(2)联立直线l和抛物线的解析式即可求出A、B的坐标.
(3)本题可通过三角形ABM的面积来求解.由于三角形AMB的面积无法直接求出,因此可将其分割成其他图形面积的和差来求解.过M作MN∥y轴交AB于N,那么三角形ABM的面积就分成了三角形AMN和BMN两部分,可以MN为底,以AB两点的横坐标的差的绝对值为高来求三角形ABM的面积,MN是抛物线的函数中与直线AB函数值的差,由此可得出关于三角形AMB的面积与M点横坐标的函数关系式.然后根据三角形ABM的面积的不同表示方法求出关于h和M点横坐标的函数关系式,根据函数的性质即可求出h的最大值.
(2)联立直线l和抛物线的解析式即可求出A、B的坐标.
(3)本题可通过三角形ABM的面积来求解.由于三角形AMB的面积无法直接求出,因此可将其分割成其他图形面积的和差来求解.过M作MN∥y轴交AB于N,那么三角形ABM的面积就分成了三角形AMN和BMN两部分,可以MN为底,以AB两点的横坐标的差的绝对值为高来求三角形ABM的面积,MN是抛物线的函数中与直线AB函数值的差,由此可得出关于三角形AMB的面积与M点横坐标的函数关系式.然后根据三角形ABM的面积的不同表示方法求出关于h和M点横坐标的函数关系式,根据函数的性质即可求出h的最大值.
解答:解:(1)∵抛物线C:y=ax2+bx+c(a≠0)过(-1,0),(0,3),(3,0);
∴可设二次函数的解析式为y=a(x+1)(x-3),
则有:3=a(0+1)(0-3),a=-1;
∴抛物线C对应的函数关系式为:y=-(x+1)(x-3)=-x2+2x+3.
(2)由
,
得:
,
;
∴A(-
,-
)和B(2,3).
(3)设点M(x,-x2+2x+3),其中-
<x<3,过点M作y轴的平行线交直线AB于点N,则N(x,
x).
且|MN|=-x2+2x+3-
x=-x2+
x+3
∴S△ABM=S△AMN+S△BMN=
|MN|(x+
)+
|MN|(2-x)
=
|MN|(
+x+2-x)
=-
x2+
x+
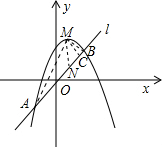
由勾股定理得:
|AB|=
=
=
.
又∵S△ABM=
|AB|•h,
∴
×
•h=-
x2+
x+
∴h=
(-x2+
x+3),
故h=-
(x-
)2+
∴当x=
(-
<
<3)时,h的最大值为
.
∴可设二次函数的解析式为y=a(x+1)(x-3),
则有:3=a(0+1)(0-3),a=-1;
∴抛物线C对应的函数关系式为:y=-(x+1)(x-3)=-x2+2x+3.
(2)由
|
得:
|
|
∴A(-
| 3 |
| 2 |
| 9 |
| 4 |
(3)设点M(x,-x2+2x+3),其中-
| 3 |
| 2 |
| 3 |
| 2 |
且|MN|=-x2+2x+3-
| 3 |
| 2 |
| 1 |
| 2 |
∴S△ABM=S△AMN+S△BMN=
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 7 |
| 4 |
| 7 |
| 8 |
| 21 |
| 4 |
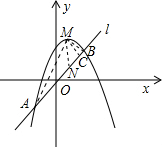
由勾股定理得:
|AB|=
(2+
|
(
|
| 7 |
| 4 |
| 13 |
又∵S△ABM=
| 1 |
| 2 |
∴
| 1 |
| 2 |
7
| ||
| 4 |
| 7 |
| 4 |
| 7 |
| 8 |
| 21 |
| 4 |
∴h=
2
| ||
| 13 |
| 1 |
| 2 |
故h=-
2
| ||
| 13 |
| 1 |
| 4 |
49
| ||
| 104 |
∴当x=
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
49
| ||
| 104 |
点评:本题主要考查了二次函数解析式的确定、函数图象交点、图形面积的求法等知识点.综合性强,难度较高.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
 16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE.
16、如图,已知直线AB和CD相交于点O,∠COE是直角,OF平分∠AOE. 5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( )
5、如图,已知直线l1∥l2,AB⊥CD,∠1=30°,则∠2的度数为( ) 如图,已知直线l1:
如图,已知直线l1: (2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2=
(2013•怀化)如图,已知直线a∥b,∠1=35°,则∠2= 如图,已知直线m∥n,则下列结论成立的是( )
如图,已知直线m∥n,则下列结论成立的是( )