��Ŀ����
��1����ͼ1������ABCD����C������ԭ��O�غϣ���A��x���ϣ���B����Ϊ��3��| 3 |
��2����ͼ2��������E��y=-
| 1 |
| 2 |
��3����ͼ3����A��B��C�ֱ�Ϊ������F��y=ax2+bx+c��a��0���ϵĵ㣬��B�ڶԳ����Ҳ࣬��D���������⣬˳������A��B��C��D�ĵ㣬�����ı���Ϊ���Σ���AC��x�ᣬAD=2CD�������ABCD���ܳ����ú�a��ʽ�ӱ�ʾ����
��������1�����ȹ���B��BH��AO��H�������Ǻ�����֪ʶ��������á�AOB�Ķ����������ı���ABCD�Ǿ��Σ�������õ�A�����꣬����Ϊ�����߹�ԭ�㣬���������߽���ʽΪy=ax2+bx�����ô���ϵ����������ô������ߵĽ���ʽ��
��2�����ݾ��������Ǻ�����֪ʶ��������õ�A��C������ֱ�Ϊ��-
y��y���루2y��y�������������߹�ԭ�㣬���c=0������A��C������������ʽ�������b��ֵ�������������ߵĽ���ʽ��
��3�������������ߣ�����B��BH��AO��H�����ΪP���������߶Գ���PQ��AC�ڵ�M����B��BN��PQ��N�������Ǻ�����֪ʶ���
=
=
�������AH=t����BH��CH��AB��BC��t��ʾ���������뺯������ʽ�������t��ֵ��������ý⣮
��2�����ݾ��������Ǻ�����֪ʶ��������õ�A��C������ֱ�Ϊ��-
| 1 |
| 2 |
��3�������������ߣ�����B��BH��AO��H�����ΪP���������߶Գ���PQ��AC�ڵ�M����B��BN��PQ��N�������Ǻ�����֪ʶ���
| AB |
| BC |
| CD |
| AD |
| 1 |
| 2 |
���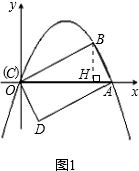 �⣺��1������B��BH��AO��H��
�⣺��1������B��BH��AO��H��
��OH=3��BH=
��
��tan��AOB=
��
���AOB=30�㣬
���ı���ABCD�Ǿ��Σ�
���ABO=90�㣬
���BAO=60�㣬
��tan��BAO=
=
��
��AH=1��
��A��4��0����
�������߹�ԭ�㣬�������߽���ʽΪy=ax2+bx��
��
����
��
��������ߵĽ���ʽΪ��y=-
x2+
x��
��2�����ı���AOCD�Ǿ��Σ�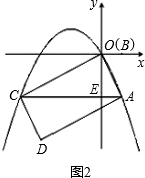
���AOC=��D=90�㣬OC��AD��
���ACO=��CAD��
��AC��x�ᣬ
���OEC=90�㣬
���AOE+��COE=��COE+��OCA=90�㣬
���AOE=��ACO=��CAD��
��Rt��ACD��tan��CAD=
��
��AD=2CD��
��tan��ACO=tan��AOE=tan��CAD=
��
�ߵ�A��C����������ͬ��
������A��������-
y��y������C��������2y��y����
�������߹�ԭ�㣬
��c=0��
�������߽���ʽΪ��y=-
x2+bx��
����A��C��������������ߵĽ���ʽ�ã�
��
��ã�b=-
��
��������ߵĽ���ʽΪ��y=-
x2-
x��
��3������B��BH��AO��H�����ΪP��
�������߶Գ���PQ��AC�ڵ�M��
��B��BN��PQ��N��
���BHC=��BHA=90�㣬
�ߡ�ABC=90�㣬
��tan��ABH=tan��ACB=
=
=
��
��AH=t����BH=2t��CH=4t��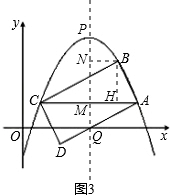
AB=
t��BC=2
t��
��y=ax2+bx+c=a��x-h��2+k��PN=n��
��A��h+
t��k-n-2t����B��h+
t��k-n����
��
��
��t1=0����ȥ����t2=-
��
��AB=-
��BC=-
��
�����ABCD���ܳ�Ϊ-
��
 �⣺��1������B��BH��AO��H��
�⣺��1������B��BH��AO��H����OH=3��BH=
| 3 |
��tan��AOB=
| ||
| 3 |
���AOB=30�㣬
���ı���ABCD�Ǿ��Σ�
���ABO=90�㣬
���BAO=60�㣬
��tan��BAO=
| BH |
| AH |
| 3 |
��AH=1��
��A��4��0����
�������߹�ԭ�㣬�������߽���ʽΪy=ax2+bx��
��
|
|
��������ߵĽ���ʽΪ��y=-
| ||
| 3 |
4
| ||
| 3 |
��2�����ı���AOCD�Ǿ��Σ�

���AOC=��D=90�㣬OC��AD��
���ACO=��CAD��
��AC��x�ᣬ
���OEC=90�㣬
���AOE+��COE=��COE+��OCA=90�㣬
���AOE=��ACO=��CAD��
��Rt��ACD��tan��CAD=
| CD |
| AD |
��AD=2CD��
��tan��ACO=tan��AOE=tan��CAD=
| 1 |
| 2 |
�ߵ�A��C����������ͬ��
������A��������-
| 1 |
| 2 |
�������߹�ԭ�㣬
��c=0��
�������߽���ʽΪ��y=-
| 1 |
| 2 |
����A��C��������������ߵĽ���ʽ�ã�
|
��ã�b=-
| 3 |
| 2 |
��������ߵĽ���ʽΪ��y=-
| 1 |
| 2 |
| 3 |
| 2 |
��3������B��BH��AO��H�����ΪP��
�������߶Գ���PQ��AC�ڵ�M��
��B��BN��PQ��N��
���BHC=��BHA=90�㣬
�ߡ�ABC=90�㣬
��tan��ABH=tan��ACB=
| AB |
| BC |
| CD |
| AD |
| 1 |
| 2 |
��AH=t����BH=2t��CH=4t��

AB=
| 5 |
| 5 |
��y=ax2+bx+c=a��x-h��2+k��PN=n��
��A��h+
| 5 |
| 2 |
| 3 |
| 2 |
��
|
��t1=0����ȥ����t2=-
| 1 |
| 2a |
��AB=-
| ||
| 2a |
| ||
| a |
�����ABCD���ܳ�Ϊ-
3
| ||
| a |
���������⿼���˴���ϵ��������κ����Ľ���ʽ�����ε����ʣ����Ǻ�����Ӧ���Լ����ı��ε��ܳ���֪ʶ�������ۺ��Ժ�ǿ���ѶȽϴ�ע�����ν���뷽��˼���Ӧ�ã�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ���ֲ�������ͼ���ھ���ֽƬABCD�У�AB=3��AD=5����ͼ��ʾ�۵�ֽƬ��ʹ��A����BC���ϵ�A�䴦���ۺ�ΪPQ������A����BC�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���������P��Q�ֱ���AB��AD�����ƶ���
���ֲ�������ͼ���ھ���ֽƬABCD�У�AB=3��AD=5����ͼ��ʾ�۵�ֽƬ��ʹ��A����BC���ϵ�A�䴦���ۺ�ΪPQ������A����BC�����ƶ�ʱ���ۺ۵Ķ˵�P��QҲ��֮�ƶ���������P��Q�ֱ���AB��AD�����ƶ��� ��ͼ��������ֽƬABCD����Խ���AC�۵���ʹ��B�䵽��B���λ�ã�AB����CD���ڵ�E��
��ͼ��������ֽƬABCD����Խ���AC�۵���ʹ��B�䵽��B���λ�ã�AB����CD���ڵ�E�� ��ͼ���ھ���ABCD�У�M��CD�е㣬AB=8��AD=3��
��ͼ���ھ���ABCD�У�M��CD�е㣬AB=8��AD=3�� ��ͼ���ھ���ABCD�У���֪AB=1��BC=2����ABC��ƽ���߽�AD�ڵ�F��EΪBC���е㣬����EF��
��ͼ���ھ���ABCD�У���֪AB=1��BC=2����ABC��ƽ���߽�AD�ڵ�F��EΪBC���е㣬����EF�� ��ͼ���ھ���ABCD�У�A��-4��1����B��0��1����C��0��3������D������Ϊ
��ͼ���ھ���ABCD�У�A��-4��1����B��0��1����C��0��3������D������Ϊ