题目内容
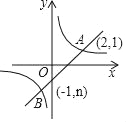
【题目】对于平面直角坐标系xOy中的点P,Q和图形G,给出如下定义:点P,Q都在图形G上,且将点P的横坐标与纵坐标互换后得到点Q,则称点P,Q是图形G的一对“关联点”.例如,点P(1,2)和点Q(2,1)是直线y=﹣x+3的一对关联点.
(1)请写出反比例函数y=![]() 的图象上的一对关联点的坐标: ;
的图象上的一对关联点的坐标: ;
(2)抛物线y=x2+bx+c的对称轴为直线x=1,与y轴交于点C(0,﹣1).点A,B是抛物线y=x2+bx+c的一对关联点,直线AB与x轴交于点D(1,0).求A,B两点坐标.
(3)⊙T的半径为3,点M,N是⊙T的一对关联点,且点M的坐标为(1,m)(m>1),请直接写出m的取值范围.
【答案】(1)(2,3),(3,2).(2)A,B两点坐标为(﹣1,2)和(2,﹣1).(3)1<m≤1+3![]() .
.
【解析】
(1)根据反比例函数性质即可写出.
(2)根据题意可求出抛物线的解析式为y=x2﹣2x﹣1, 直线AB与x轴交于点D(1,0)得到直线AB的解析式为y=﹣x+1,联立直线AB及抛物线解析式成方程组即可解出A,B两点坐标.
(3)点M,N关于直线y=x对称得到⊙T的圆心在直线y=x上,进而求得M1M2的值即可求出m的取值范围.
解:(1)∵2×3=3×2=6,
∴点(2,3),(3,2)是反比例函数y=![]() 的图象上的一对关联点.
的图象上的一对关联点.
故答案为:(2,3),(3,2).
(2)∵抛物线y=x2+bx+c的对称轴为直线x=1,
∴﹣![]() =1,
=1,
解得:b=﹣2.
∵抛物线y=x2+bx+c与y轴交于点C(0,﹣1),
∴c=﹣1,
∴抛物线的解析式为y=x2﹣2x﹣1.
由关联点定义,可知:点A,B关于直线y=x对称.
又∵直线AB与x轴交于点D(1,0),
∴直线AB的解析式为y=﹣x+1.
联立直线AB及抛物线解析式成方程组,得:![]() ,
,
解得:![]() ,
,![]() ,
,
∴A,B两点坐标为(﹣1,2)和(2,﹣1).
(3)由关联点定义,可知:点M,N关于直线y=x对称,
∴⊙T的圆心在直线y=x上.
∵⊙T的半径为3,
∴M1M2=![]() ×2×3=3
×2×3=3![]() ,
,
∴m的取值范围为1<m≤1+3![]() .
.

【题目】下表显示了同学们用计算机模拟随机投针实验的某次实验的结果.
投针次数n | 1000 | 2000 | 3000 | 4000 | 5000 | 10000 | 20000 |
针与直线相交的次数m | 454 | 970 | 1430 | 1912 | 2386 | 4769 | 9548 |
针与直线相交的频率p=
| 0.454 | 0.485 | 0.4767 | 0.478 | 0.4772 | 0.4769 | 0.4774 |
下面有三个推断:
①投掷1000次时,针与直线相交的次数是454,针与直线相交的概率是0.454;
②随着实验次数的增加,针与直线相交的频率总在0.477附近,显示出一定的稳定性,可以估计针与直线相交的概率是0.477;
③若再次用计算机模拟此实验,则当投掷次数为10000时,针与直线相交的频率一定是0.4769.
其中合理的推断的序号是:_____.