Ő‚ńŅńŕ»›
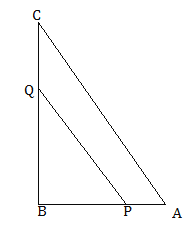
°ĺŐ‚ńŅ°Ņį—ĪŖ≥§∑÷Īūő™4ļÕ6Ķńĺō–őABCO»ÁÕľ∑Ň‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨ĹęňŁ»∆Ķ„Cň≥ Ī’Ž–ż◊™aĹ«£¨–ż◊™ļůĶńĺō–őľ«ő™ĺō–őEDCF£ģ‘ŕ–ż◊™Ļż≥Ő÷–£¨
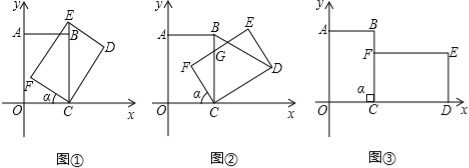
£®1£©»ÁÕľĘŔ£¨ĶĪĶ„E‘ŕ…šŌŖCB…Ō Ī£¨EĶ„◊ÝĪÍő™ £Ľ
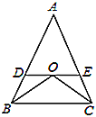
£®2£©ĶĪ°ųCBD «Ķ»ĪŖ»żĹ«–ő Ī£¨–ż◊™Ĺ«aĶń∂» ż « £®aő™»ŮĹ« Ī£©£Ľ
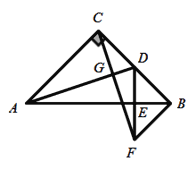
£®3£©»ÁÕľĘŕ£¨…ŤEF”ŽBCĹĽ”ŕĶ„G£¨ĶĪEG=CG Ī£¨«ůĶ„GĶń◊ÝĪÍ£Ľ
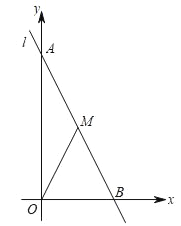
£®4£©»ÁÕľĘŘ£¨ĶĪ–ż◊™Ĺ«a=90°„ Ī£¨«ŽŇ–∂Ōĺō–őEDCFĶń∂‘≥∆÷––ńH «∑Ů‘ŕ“‘Cő™∂•Ķ„£¨«“ĺ≠ĻżĶ„AĶńŇ◊őÔŌŖ…Ō£ģ
°ĺīūįł°Ņ£®1£©E£®4£¨2![]() £©£Ľ
£©£Ľ
£®2£©60°„£Ľ
£®3£©![]() £Ľ
£Ľ
£®4£©Ķ„H≤Ľ‘ŕīňŇ◊őÔŌŖ…Ō£ģ
°ĺĹ‚őŲ°Ņ
‘Ő‚£®1£©“ņŐ‚“‚Ķ√Ķ„E‘ŕ…šŌŖCB…Ō£¨ļŠ◊ÝĪÍő™4£¨◊›◊ÝĪÍłýĺ›ĻīĻ…∂®ņŪŅ…Ķ√Ķ„E£ģ
£®2£©“—÷™°ŌBCD=60°„£¨°ŌBCF=30°„£¨»ĽļůŅ…Ķ√°Ō¶Ń=60°„£ģ
£®3£©…ŤCG=x£¨‘ÚEG=x£¨FG=6©Āx£¨łýĺ›ĻīĻ…∂®ņŪ«ů≥ŲCGĶń÷Ķ£ģ
£®4£©…Ť“‘Cő™∂•Ķ„ĶńŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™y=a£®x©Ā4£©2£¨į—Ķ„AĶń◊ÝĪÍīķ»Ž«ů≥Ųa÷Ķ£ģĶĪx=7 Īīķ»ŽļĮ żĹ‚őŲ ĹŅ…Ķ√Ĺ‚£ģ
Ĺ‚£ģ£®1£©E£®4£¨2![]() £©
£©
£®2£©60°„
£®3£©…ŤCG=x£¨‘ÚEG=x£¨FG=6©Āx£¨
‘ŕRt°ųFGC÷–£¨°ŖCF2+FG2=CG2£¨
°ŗ42+£®6©Āx£©2=x2
Ĺ‚Ķ√![]() £¨ľī
£¨ľī![]()
°ŗ![]()
£®4£©…Ť“‘Cő™∂•Ķ„ĶńŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™y=a£®x©Ā4£©2£¨
į—A£®0£¨6£©īķ»Ž£¨Ķ√6=a£®0©Ā4£©2£ģ
Ĺ‚Ķ√a=![]() £ģ
£ģ
°ŗŇ◊őÔŌŖĶńĹ‚őŲ Ĺő™y=![]() £®x©Ā4£©2
£®x©Ā4£©2
°Ŗĺō–őEDCFĶń∂‘≥∆÷––ńHľīő™∂‘Ĺ«ŌŖFD°ĘCEĶńĹĽĶ„£¨
°ŗH£®7£¨2£©£ģ
ĶĪx=7 Ī£¨![]()
°ŗĶ„H≤Ľ‘ŕīňŇ◊őÔŌŖ…Ō£ģ

 įŔńÍ—ßĶšŅő Ī—ßŃ∑≤‚ŌĶŃ–īūįł
įŔńÍ—ßĶšŅő Ī—ßŃ∑≤‚ŌĶŃ–īūįł » įģ”Ę”ÔÕ¨≤ĹŃ∑Ōį≤ŠŌĶŃ–īūįł
» įģ”Ę”ÔÕ¨≤ĹŃ∑Ōį≤ŠŌĶŃ–īūįł —ßŌį Ķľý‘įĶōŌĶŃ–īūįł
—ßŌį Ķľý‘įĶōŌĶŃ–īūįł