题目内容
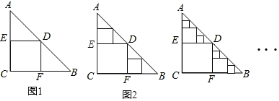
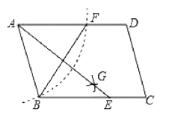
【题目】如图,某仓储中心有一斜坡AB,其坡比为i=1∶2,顶部A处的高AC为4 m,B,C在同一水平面上.
(1)求斜坡AB的水平宽度BC;
(2)矩形DEFG为长方形货柜的侧面图,其中DE=2.5 m,EF=2 m.将货柜沿斜坡向上运送,当BF=3.5 m时,求点D离地面的高.(![]() ≈2.236,结果精确到0.1 m)
≈2.236,结果精确到0.1 m)

【答案】(1) BC=8 m;(2)点D离地面的高为4.5 m.
【解析】
试题(1)根据坡度定义直接解答即可;
(2)作DS⊥BC,垂足为S,且与AB相交于H.证出∠GDH=∠SBH,根据![]() ,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.
,得到GH=1m,利用勾股定理求出DH的长,然后求出BH=5m,进而求出HS,然后得到DS.
试题解析:(1)∵坡度为i=1:2,AC=4m,
∴BC=4×2=8m.
(2)作DS⊥BC,垂足为S,且与AB相交于H.

∵∠DGH=∠BSH,∠DHG=∠BHS,
∴∠GDH=∠SBH,
![]()
∵DG=EF=2m,
∴GH=1m,
∴DH=![]() m,BH=BF+FH=3.5+(2.5-1)=5m,
m,BH=BF+FH=3.5+(2.5-1)=5m,
设HS=xm,则BS=2xm,
∴x2+(2x)2=52,
∴x=![]() m,
m,
∴DS=![]() +
+![]() =2
=2![]() m≈4.5m.
m≈4.5m.

练习册系列答案
相关题目