题目内容
【题目】已知,![]() ,
,![]() 分别在直线
分别在直线![]() 上,
上,![]() 是平面内一点,
是平面内一点,![]() 和
和![]() 的平分线所在直线相交于点
的平分线所在直线相交于点![]() .
.
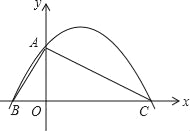
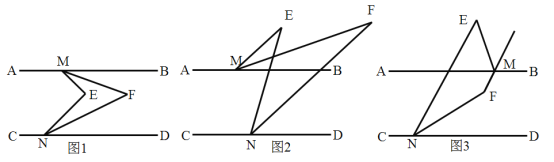
(1)如图1,当![]() 都在直线
都在直线![]() 之间,且
之间,且![]() 时,
时,![]() 的度数为_________;
的度数为_________;
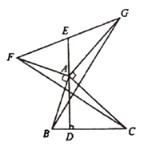
(2)如图2,当![]() 都在直线
都在直线![]() 上方时,探究
上方时,探究![]() 和
和![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
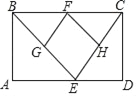
(3)如图3,当![]() 在直线
在直线![]() 两侧时,直接写出
两侧时,直接写出![]() 和
和![]() 之间的数量关系是_____.
之间的数量关系是_____.
【答案】(1)45°;(2)证明见解析;(3)![]() .
.
【解析】
(1)过E作EH∥AB,FG∥AB,根据平行线的性质得到∠BME=∠MEH,∠DNE=∠NEH,根据角平分线的定义得到∠BMF+∠DNF=![]() (∠BME+∠DNE)=45°,于是得到结论;(2)根据三角形的外角的性质得到∠E=∠EGB-∠EMB,根据平行线的性质得到∠EGB=∠END,∠FHB=∠FND,根据角平分线的定义得到∠EMB=2∠FMB,∠END=2∠FND,于是得到结论;(3)根据平行线的性质得到∠5=∠END,根据角平分线的定义得到∠5=∠END=2∠4,∠BME=2∠1=∠E+∠5=∠E+2∠4,根据三角形的外角的性质和四边形的内角和即可得到结论.
(∠BME+∠DNE)=45°,于是得到结论;(2)根据三角形的外角的性质得到∠E=∠EGB-∠EMB,根据平行线的性质得到∠EGB=∠END,∠FHB=∠FND,根据角平分线的定义得到∠EMB=2∠FMB,∠END=2∠FND,于是得到结论;(3)根据平行线的性质得到∠5=∠END,根据角平分线的定义得到∠5=∠END=2∠4,∠BME=2∠1=∠E+∠5=∠E+2∠4,根据三角形的外角的性质和四边形的内角和即可得到结论.
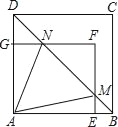
解:(1)过E作EH∥AB,过点F作FG∥AB,
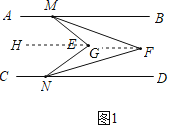
∵AB∥CD,
∴EH∥CD,FG∥CD,
∴∠BME=∠MEH,∠DNE=∠NEH,
∴∠BME+∠DNE=∠MEH+∠NEH=∠MEN=90°,
同理∠MFN=∠BMF+∠DNF,
∵MF平分∠BME,FN平分∠DNE,
∴∠BMF+∠DNF=![]() (∠BME+∠DNE)=45°,
(∠BME+∠DNE)=45°,
∴∠MFN的度数为45°;
故答案为:45°;
(2)∵∠EGB=∠EMB+∠E,
∴∠E=∠EGB-∠EMB,
∵AB∥CD,
∴∠EGB=∠END,∠FHB=∠FND,
∴∠E=∠END-∠EMB,
∵MF、NF分别平分∠BME和∠DNE,
∴∠EMB=2∠FMB,∠END=2∠FND,
∴∠E=2∠FND-2∠FMB=2(∠FND-∠FMB),
∵∠FHB=∠FMB+∠F,
∴∠F=∠FHB-∠FMB,
=∠FND-∠FMB,
∴∠E=2∠F;
(3)![]() ∠E+∠MFN=180°,
∠E+∠MFN=180°,
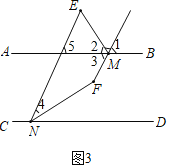
证明:∵AB∥CD,
∴∠5=∠END,
∵NF平分∠END,
∴∠5=∠END=2∠4,
∵MF平分∠BME,
∴∠BME=2∠1=∠E+∠5=∠E+2∠4,
∴∠3=∠1=![]() ∠E+∠4,
∠E+∠4,
∵∠E+∠MFN=360°-∠4-∠2-∠3=360°-∠4-(180°-∠E-2∠4)-(![]() ∠E+∠4)=180°+
∠E+∠4)=180°+![]() ∠
∠
∴∠MFN+![]() ∠E=180°.
∠E=180°.
故答案为:![]() ∠E+∠MFN=180°.
∠E+∠MFN=180°.