题目内容
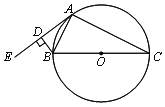
【题目】如图,在△ABC中,BC=AC=6,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)求点O到直线DE的距离.

【答案】(1)证明见解析(2)3
【解析】
(1)连接![]() ,由
,由![]() 为直径可知
为直径可知![]() ,又因为
,又因为![]() ,由等腰三角形的底边“三线合一”证明结论;
,由等腰三角形的底边“三线合一”证明结论;
(2)连接![]() ,则
,则![]() 为
为![]() 的中位线,
的中位线,![]() ,已知
,已知![]() ,即可知
,即可知![]() 的长即为点
的长即为点![]() 到直线
到直线![]() 的距离.
的距离.
(1)如图,连接CD,
∵BC是⊙O的直径,
∴∠BDC=90°.
∴CD⊥AB,
又∵AC=BC,
∴AD=BD,即点D是AB的中点.
(2)如图,连接OD,
∵AD=BD,OB=OC,
∴DO是△ABC的中位线.
∴DO∥AC,OD=![]() AC=3.
AC=3.
又∵DE⊥AC,
∴DE⊥DO.
∴点O到直线DE的距离为3.

练习册系列答案
相关题目
【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?