题目内容
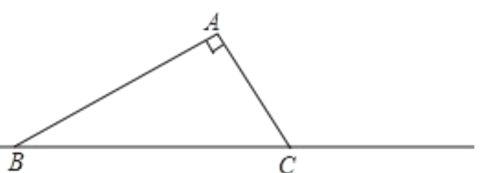
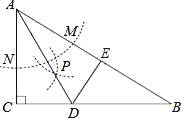
【题目】如图，在Rt△ABC中，∠C=90°，∠B=30°，以A为圆心适当长为半径画弧，分别交AC、AB于点M、N，分别以点M、N为圆心，大于
MN的长为半径画弧交于点P，作射线AP交BC于点D，再作射线DE交AB于点E，则下列结论错误的是（ ）
A. ∠ADB=120° B. S△ADC：S△ABC=1：3
C. 若CD=2，则BD=4 D. DE垂直平分AB
【答案】D
【解析】分析：根据题意得出AD为∠CAB的平分线，然后根据平分线的性质得出答案．
详解：∵∠B=30°，∠C=90°，AD平分∠CAB， ∴∠CAD=∠DAB=30°，则∠ADB=120°，
则A正确；当CD=2时，根据角平分线的性质可得：DE=2，BD=4，则C正确；△ACD的面积=AC×CD÷2，△ABC的面积=AC×BC÷2，则S△ADC：S△ABC=1：3，故B正确；DE垂直AB，故D错误；则本题选择D．
练习册系列答案
相关题目
