题目内容
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与正比例函数
,与正比例函数![]() 的图象交于点
的图象交于点![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且点
轴的正半轴上,且点![]() 的横坐标为
的横坐标为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,分别交一次函数
轴的垂线,分别交一次函数![]() 的图象于点
的图象于点![]() ,交正比例函数
,交正比例函数![]() 的图象于点
的图象于点![]() .
.
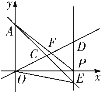
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 为何值时,
为何值时,![]() ;
;
(3)连接![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,在讨论
,在讨论![]() 的面积与
的面积与![]() 面积的大小问题时,嘉嘉认为
面积的大小问题时,嘉嘉认为![]() ,淇淇认为
,淇淇认为![]() ,请你作为小法官,帮助他们两人评判,谁的说法正确.
,请你作为小法官,帮助他们两人评判,谁的说法正确.
【答案】(1)点C的坐标为![]() ;(2)当
;(2)当![]() 时,
时,![]() ;(3)淇淇的说法正确.理由见解析
;(3)淇淇的说法正确.理由见解析
【解析】
解:(1)联立一次函数![]() 和正比例函数
和正比例函数![]() ,
,
可得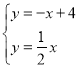 ,解得
,解得![]() ,
,
∴点C的坐标为![]() ;
;
(2)∵一次函数![]() 的图象与y轴的交点为A,
的图象与y轴的交点为A,
∴点A的坐标为![]() ,即
,即![]() ,
,
∵点C的坐标为![]() ,
,
∴![]() ,
,
∵点D的横坐标为m,且点D在正比例函数![]() 的图象上,
的图象上,
∴可设点D的坐标为![]() ,则点E的坐标为
,则点E的坐标为![]() ,
,
∴![]() ,
,
∵当![]() 时,不存在
时,不存在![]() ,
,
∴![]() ,
,
∴点C到DE的距离为![]() ,
,
∴![]() ,解得
,解得![]() ,
,![]() (舍去),
(舍去),
∴当![]() 时,
时,![]() ;
;
(3)淇淇的说法正确.
理由:∵![]() ,
,
∴点F在OC的延长线上,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴淇淇的说法正确.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)