题目内容
【题目】如图,已知在△ABC中,AB=15,AC=20,tanA=![]() ,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
,点P在AB边上,⊙P的半径为定长.当点P与点B重合时,⊙P恰好与AC边相切;当点P与点B不重合时,⊙P与AC边相交于点M和点N.
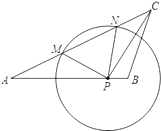
(1)求⊙P的半径;
(2)当AP=![]() 时,试探究△APM与△PCN是否相似,并说明理由.
时,试探究△APM与△PCN是否相似,并说明理由.
【答案】(1)半径为3![]() ;(2)相似,理由见解析.
;(2)相似,理由见解析.
【解析】(1)如图,作BD⊥AC,垂足为点D,⊙P与边AC相切,则BD就是⊙P的半径,利用解直角三角形得出BD与AD的关系,再利用勾股定理可求得BD的长;
(2)如图,过点P作PH⊥AC于点H,作BD⊥AC,垂足为点D,根据垂径定理得出MN=2MH,PM=PN,再利用勾股定理求出PH、AH、MH、MN的长,从而求出AM、NC的长,然后求出![]() 、
、![]() 的值,得出
的值,得出![]() =
=![]() ,利用两边对应成比例且夹角相等的两三角形相似即可证明.
,利用两边对应成比例且夹角相等的两三角形相似即可证明.
(1)如图,作BD⊥AC,垂足为点D,
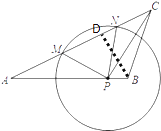
∵⊙P与边AC相切,
∴BD就是⊙P的半径,
在Rt△ABD中,tanA= ![]() ,
,
设BD=x,则AD=2x,
∴x2+(2x)2=152,
解得:x=3![]() ,
,
∴半径为3![]() ;
;
(2)相似,理由见解析,
如图,过点P作PH⊥AC于点H,作BD⊥AC,垂足为点D,
∴PH垂直平分MN,
∴PM=PN,
在Rt△AHP中,tanA=![]() ,
,
设PH=y,AH=2y,
y2+(2y)2=(6![]() )2
)2
解得:y=6(取正数),
∴PH=6,AH=12,
在Rt△MPH中,
MH=![]() =3,
=3,
∴MN=2MH=6,
∴AM=AH-MH=12-3=9,
NC=AC-MN-AM=20-6-9=5,
∴![]() ,
,![]() ,
,
∴![]() =
=![]() ,
,
又∵PM=PN,
∴∠PMN=∠PNM,
∴∠AMP=∠PNC,
∴△AMP∽△PNC.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目