题目内容
【题目】计算题
1、计算、
+（
）﹣1﹣4tan45° 2、 解方程：x2=3x．
（1）计算： +（ ）﹣1﹣4tan45°
（2）解方程：x2=3x．
【答案】
（1）解：原式=2 
+2﹣4× 
=2
（2）解：x2=3x，
x2﹣3x=0
x（x﹣3）=0
x=0，x﹣3=0
x1=0，x2=3
【解析】（1）先算乘方、开方，再算乘除，最后算加减法。注意：负整数指数幂的运算，底数变倒数，同时指数由负整数变成正整数。
【考点精析】认真审题，首先需要了解整数指数幂的运算性质(aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数))，还要掌握最简二次根式(最简根式三条件，号内不把分母含，幂指（数）根指（数）要互质，幂指比根指小一点)的相关知识才是答题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】我市某中学举行十佳歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图所示．
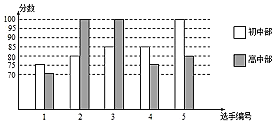
（1）根据所给信息填空：
平均数（分） | 中位数（分） | 众数（分） | 方差 | |
初中部 | 85 | ______ | 85 | _______ |
高中部 | _____ | 80 | ______ | 160 |
（2）你觉得高中部和初中部的决赛成绩哪个更好？说明理由．
