Question

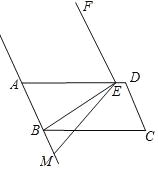
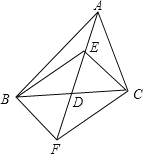
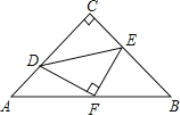
【题目】如图，已知△ABC中，AC=BC，∠ACB=90°，直角∠DFE的顶点F是AB中点，两边FD，FE分别交AC，BC于点D，E两点，当∠DFE在△ABC内绕顶点F旋转时（点D不与A，C重合），给出以下个结论：①CD=BE；②四边形CDFE不可能是正方形；③△DFE是等腰直角三角形；④S四边形CDFE=S△ABC．上述结论中始终正确的有______．（填序号）

Answer 1

【答案】①③④

【解析】

首先连接CF，由等腰直角三角形的性质可得：，则证得∠DCF=∠B，∠DFC=∠EFB，然后可证得：△DCF≌△EBF，由全等三角形的性质可得CD=BE，DF=EF，也可证得S四边形CDFE=S△ABC．问题得解．

解：连接CF，

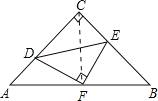
∵AC=BC，∠ACB=90°，点F是AB中点，

∴∠DCF=∠B=45°，
∵∠DFE=90°，
∴∠DFC+∠CFE=∠CFE+∠EFB=90°，
∴∠DFC=∠EFB，
∴△DCF≌△EBF，
∴CD=BE，故①正确；
∴DF=EF，
∴△DFE是等腰直角三角形，故③正确；
∴S△DCF=S△BEF，
∴S四边形CDFE=S△CDF+S△CEF=S△EBF+S△CEF=S△CBF=S△ABC．，故④正确．
若EF⊥BC时，则可得：四边形CDFE是矩形，
∵DF=EF，
∴四边形CDFE是正方形，故②错误．
∴结论中始终正确的有①③④．
故答案为：①③④．