��Ŀ����
����Ŀ��Ϊ�������������С���İְ�Ҫ��Ժǽ���һ��յ�����һ�����λ��ԣ���ͼ��ʾ�����λ��Ե�һ�����ó�10��Ժǽ�����������������Χ�ɣ���ʵ��ܳ�Ϊ32�ף���AB�ij�Ϊx�ף����λ��Ե����Ϊyƽ���ף�
��1���ú���x�Ĵ���ʽ��ʾBC�ij���BC=�� ����
��2����y��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
��3����xΪ��ֵʱ��y�����ֵ�����ֵΪ���٣�
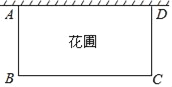
���𰸡���1��32-2x����2��y=-2x2+32x(11��x��16)����3����x=11ʱ��y���=110(m2)
�����������������(1)�������ܳ���ȥAB��CD�Ϳ��Եó��𰸣�(2)�����ݾ��ε�������㷨��ó���������ʽ������![]() ���ȡֵ��Χ��(3)�����Ƚ����������䷽��Ȼ�����������������ֵ��
���ȡֵ��Χ��(3)�����Ƚ����������䷽��Ȼ�����������������ֵ��
���������(1)��BC=32-2x��
(2)��y=x(32-2x)=![]() �� ���������֪��
�� ���������֪��![]()
��ã�![]() ��
��
(3)��![]() ��
��
��![]() ʱ��y����x���������С������������֪����x=11ʱ��y�����ֵ��
ʱ��y����x���������С������������֪����x=11ʱ��y�����ֵ��
���ֵΪ��![]() ��
��

��ϰ��ϵ�д�
�����Ŀ