题目内容
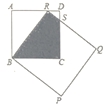
【题目】正方形ABCD和正方形BPQR的面积分别为16、25,它们重叠的情形如图所示,其中R点在AD上,CD与QR相交于S点,则四边形RBCS的面积为( )
A. 8B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
根据正方形的边长,根据勾股定理求出AR,求出△ABR∽△DRS,求出DS,根据面积公式求出即可.
∵正方形ABCD的面积为16,正方形BPQR面积为25,
∴正方形ABCD的边长为4,正方形BPQR的边长为5,
在Rt△ABR中,AB=4,BR=5,由勾股定理得:AR=3,
∵四边形ABCD是正方形,
∴∠A=∠D=∠BRQ=90°,
∴∠ABR+∠ARB=90°,∠ARB+∠DRS=90°,
∴∠ABR=∠DRS,
∵∠A=∠D,
∴△ABR∽△DRS,
∴![]() ,
,
∴![]() ,
,
∴DS=![]() ,
,
∴∴阴影部分的面积S=S正方形ABCD-S△ABR-S△RDS=4×4-![]() ×4×3-
×4×3-![]() ×
×![]() ×1=
×1=![]() ,
,
故选:D.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由
【题目】阅读材料:
工厂加工某种新型材料,首先要将材料进行加温处理,使这种材料保持在一定的温度范围内方可进行继续加工![]() 处理这种材料时,材料温度
处理这种材料时,材料温度![]() 是时间
是时间![]() 的函数
的函数![]() 下面是小明同学研究该函数的过程,把它补充完整:
下面是小明同学研究该函数的过程,把它补充完整:
![]() 在这个函数关系中,自变量x的取值范围是______.
在这个函数关系中,自变量x的取值范围是______.
![]() 如表记录了17min内10个时间点材料温度y随时间x变化的情况:
如表记录了17min内10个时间点材料温度y随时间x变化的情况:
时间 | 0 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 |
|
温度 | 15 | 24 | 42 | 60 |
|
|
|
| m |
|
|
上表中m的值为______.
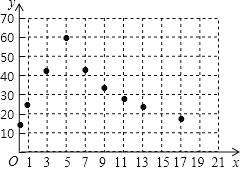
![]() 如图,在平面直角坐标系xOy中,已经描出了上表中的部分点
如图,在平面直角坐标系xOy中,已经描出了上表中的部分点![]() 根据描出的点,画出该函数的图象.
根据描出的点,画出该函数的图象.
![]() 根据列出的表格和所画的函数图象,可以得到,当
根据列出的表格和所画的函数图象,可以得到,当![]() 时,y与x之间的函数表达式为______,当
时,y与x之间的函数表达式为______,当![]() 时,y与x之间的函数表达式为______.
时,y与x之间的函数表达式为______.
![]() 根据工艺的要求,当材料的温度不低于
根据工艺的要求,当材料的温度不低于![]() 时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.
时,方可以进行产品加工,在图中所示的温度变化过程中,可以进行加工的时间长度为______min.


