题目内容
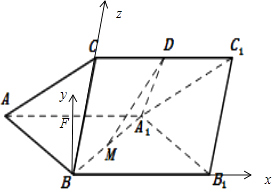
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面ABB1A1为菱形且 ![]() ,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1.
,D,M分别为CC1和A1B的中点,A1D⊥CC1 , AA1=A1D=2,BC=1. 
(Ⅰ)证明:直线MD∥平面ABC;
(Ⅱ)求二面角B﹣AC﹣A1的余弦值.
【答案】解:∵A1D⊥CC1 , 且D为中点,AA1=A1D=2,∴ ![]() , 又 BC=1,AB=BA1=2,∴CB⊥BA,CB⊥BA1 ,
, 又 BC=1,AB=BA1=2,∴CB⊥BA,CB⊥BA1 ,
又 BA∩BA1=B,∴CB⊥平面ABB1A1 ,
取AA1中点F,则BF⊥AA1 , 即BC,BF,BB1两两互相垂直,
以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系如图所示,B1(2,0,0),C(0,0,1), ![]() ,
, ![]() ,C1(2,0,1),D(1,0,1),
,C1(2,0,1),D(1,0,1), 
(I) 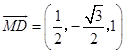 ,设平面ABC的法向量为
,设平面ABC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 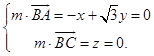 ,取
,取 ![]() ,
,
∵ ![]() ,∴
,∴ ![]() ,
,
又MD平面ABC,∴直线MD∥平面ABC.
(II) 设平面ACA1的法向量为n=(x1 , y1 , z1), ![]() ,
,
则 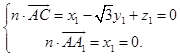 ,取
,取 ![]() ,
,
又由(Ⅰ)知平面ABC的法向量为 ![]() ,
,
设二面角B﹣AC﹣A1为θ,
∴ 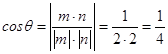 ,
,
∴二面角B﹣AC﹣A1的余弦值为 ![]()
【解析】由已知可得 ![]() ,CB⊥平面ABB1A1 , 取AA1中点F可得BC,BF,BB1两两互相垂直 以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系,B1(2,0,0),C(0,0,1),
,CB⊥平面ABB1A1 , 取AA1中点F可得BC,BF,BB1两两互相垂直 以B为原点,BB1 , BF,BC分别为x,y,z轴,建立空间直角坐标系,B1(2,0,0),C(0,0,1), ![]() ,
, ![]() ,C1(2,0,1),D(1,0,1),
,C1(2,0,1),D(1,0,1), ![]() ,利用空间向量求解.
,利用空间向量求解.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目