题目内容
【题目】已知直线y=x+m与抛物线x2=4y相切，且与x轴的交点为M，点N（﹣1，0）．若动点P与两定点M，N所构成三角形的周长为6．
（Ⅰ）求动点P的轨迹C的方程；
（Ⅱ） 设斜率为 
的直线l交曲线C于A，B两点，当PN⊥MN时，证明：∠APN=∠BPN．
【答案】解：（Ⅰ）∵直线y=x+m与抛物线x2=4y相切，
∴方程x2=4（x+m）有等根，
∴△=16+16m=0，解得m=﹣1，∴M（1，0），
又∵动点P与定点M（1，0），N（﹣1，0）所构成的三角形的周长为6，且|MN|=2，
∴|PM|+|PN|=4＞|MN|=2，
根据椭圆的定义，动点在以M，N为焦点的椭圆上，且不在x轴上，
∴2a=4，2c=2，解得a=2，c=1，∴b= 
，
∴动点P的轨迹C的方程为 
=1（y≠0）．
（Ⅱ）证明：设直线l的方程为y= 
，（t≠±1），
联立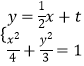 
，得x2+tx+t2﹣3=0，
△′=﹣3t2+12＞0，∴﹣2＜t＜2，此时直线l与曲线C有两个交点A，B，
设A（x1 ， y1），B（x2 ， y2），则 
，
∵PN⊥MN，不妨取P（1， 
），
要证明∠APN=∠BPN，也就是要证明kAP+kBP=0，
即证 
+ 
=0，即证（ 
）（x2﹣1）+（y2﹣ ）（x1﹣1）=0，
即证x1x2+t（x1+x2）﹣2（x1+x2）+3﹣2t=0，
把 ，代入，得：
t2﹣3﹣t2+2t+3﹣2t=0，
∴∠APN=∠BPN．
【解析】（Ⅰ）由直线y=x+m与抛物线x2=4y相切，利用根的差别式求出m=﹣1，从而M（1，0），进而推导出动点在以M，N为焦点的椭圆上，且不在x轴上，由此能求出动点P的轨迹C的方程．（Ⅱ）设直线l的方程为y= ，（t≠±1），联立 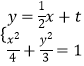，得x2+tx+t2﹣3=0，由根的判别式得到﹣2＜t＜2，要证明∠APN=∠BPN，即要证明kAP+kBP=0，即证x1x2+t（x1+x2）﹣2（x1+x2）+3﹣2t=0，由此利用韦达定理能证明∠APN=∠BPN．
