��Ŀ����
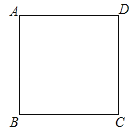
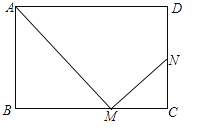
����Ŀ���ھ���ABCD�У�AB=a��AD=b����MΪBC����һ���㣨��M���B��C���غϣ�������AM������M��MN��AM������ΪM��MN��CD��CD���ӳ����ڵ�N��
��1����֤����CMN�ס�BAM��
��2����BM=x��CN=y����y����x�ĺ�������ʽ����xȡ��ֵʱ��y�����ֵ�������y�����ֵ��
��3������M��BC���˶�ʱ����ʹ����������������������b��ȡֵ��Χ���ٵ�Nʼ�����߶�CD�ϣ��ڵ�M��ijһλ��ʱ����Nǡ�����D�غϣ�
���𰸡���1��֤���������������2��![]() ����x=
����x=![]() ʱ��yȡ���ֵ��Ϊ
ʱ��yȡ���ֵ��Ϊ![]() ����3��b=2a��
����3��b=2a��
��������
�����������1���ɾ����������ɵ���B=��C=90�㣬Ҫ֤��CMN�ס�BAM��ֻ��֤��BAM=��CMN���ɣ�
��2������CMN�ס�BAM���ɵõ�y��x�ĺ�������ʽ��Ȼ��ֻ�������䷽���Ϳ����y�����ֵ��
��3���ɵ�M��BC���˶�����M���B��C���غϣ����ɵ�0��x��b��Ҫ���������٣�Ӧ��֤��0��x��bʱ��y��a�������Ҫ���������ڣ������һ��x��ʹ��y=a���ۺ������ٺ͢ڣ���0��x��bʱy���ֵӦΪa��Ȼ���ϣ�2���еĽ��ۣ��Ϳɽ�����⣮
�����������1�����ı���ABCD�Ǿ��Σ����B=��C=90�㣬���BAM+��AMB=90�㣮��MN��AM������AMN=90�㣬���CMN+��AMB=90�㣬���BAM=��CMN�����CMN�ס�BAM��
��2���ߡ�CMN�ס�BAM����![]() ����BM=x��CN=y��AB=a��BC=AD=b����
����BM=x��CN=y��AB=a��BC=AD=b����![]() ����
����![]() =
=![]() ����
����![]() ��0������x=
��0������x=![]() ʱ��yȡ���ֵ�����ֵΪ
ʱ��yȡ���ֵ�����ֵΪ![]() ��
��
��3�������֪����0��x��bʱ��y�����ֵΪa����![]() =a����ã�b=2a����Ҫͬʱ��������������b��ֵΪ2a��
=a����ã�b=2a����Ҫͬʱ��������������b��ֵΪ2a��

 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д� �㾦�½̲�ȫ�ܽ��ϵ�д�
�㾦�½̲�ȫ�ܽ��ϵ�д�����Ŀ��������ij��ѧ��չ����Ϊ���Ұ��Ķ�����ר��������˽�ѧУ1200��ѧ��һ�����Ķ��鼮�������������ȡ����ѧ������ͳ�ƣ����Ƴ�������δ��ɵ�Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ�������ͼ���������������⣺
���� | Ƶ�� | Ƶ�� |
0��x��5 | 4 | 0.08 |
5��x��10 | 14 | 0.28 |
10��x��15 | 16 | a |
15��x��20 | b | c |
20��x��25 | 10 | 0.2 |
�ϼ� | d | 1.00 |
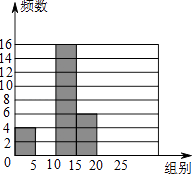
��1��a= �� b= �� c= �� d= ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3�����ݸ����������Ƹ�Уѧ���Ķ��鼮������15�������ϵ�������
��4������Ķ��鼮������10�������ϵ�����ռ��������70%���ϣ���ô��У����Ϊ������У����������������ݷ�����У�Ƿ��ܻ�ô���������˵�����ɣ�