题目内容
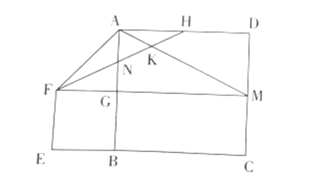
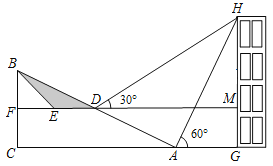
【题目】如图,坡AB的坡度为1:2.4,坡面长26米,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE(请将下面两小题的结果都精确到0.1米,参考数据:![]() ≈1.732).
≈1.732).
(1)若修建的斜坡BE的坡角(即∠BEF)恰为45°,则此时平台DE的长为 米;
(2)坡前有一建筑物GH,小明在D点测得建筑物顶部H的仰角为30°,在坡底A点测得建筑物顶部H的仰角为60°,点B、C、A、G、H在同一平面内,点C、A、G在同一条水平直线上,问建筑物GH高为多少米?
【答案】(1)7;(2)建筑物GH高约为17.9米.
【解析】
(1)由勾股定理分别求出BC,AC的长,再证明DF是△ABC的中位线,求出DF、BF的长,即可得出答案;
(2)过点D作DP⊥AC,垂足为P,解直角三角形即可得到结论.
解:(1)∵坡AB的坡度为1:2.4,坡面长26米,
设BC=x米,则AC=2.4x米,
由![]() ,得
,得 ![]()
解得,x=10,或x=-10(舍去)
∴BC=10,AC=24,
∵修建的斜坡BE的坡角∠BEF=45°,D为AB的中点,
∴AD=BD=13,
∵DF//AC,
∴DF为△ABC的中位线,
∴BF=CF=EF=![]() BC=5,DF=
BC=5,DF=![]() AC=12,
AC=12,
故:DE=DF﹣EF=12﹣5=7(米);
则平台DE的长为7m,
故答案为:7;
(2)过点D作DP⊥AC,垂足为P.
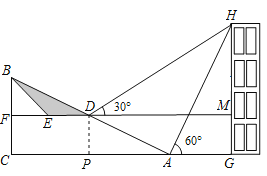
在Rt△DPA中,DP=CF=5,
PA=![]() AC=12,
AC=12,
在矩形DPGM中,MG=DP=12,DM=PG=12+AG,
在Rt△DMH中,
HM=DMtan30°=![]() ×(12+AG),
×(12+AG),
GH=HM+MG=![]() ×(12+AG)+5,
×(12+AG)+5,
∵∠HAG=60°,
∴tan60°=![]() =
=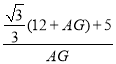 =
=![]() ,
,
解得:AG=![]() ,
,
∴HG=![]() AG=
AG=![]() ≈17.9(米),
≈17.9(米),
答:建筑物GH高约为17.9米.
【点题】
此题主要考查了解直角三角形中坡角问题,根据图象构建直角三角形,进而利用锐角三角函数得出是解题关键.