��Ŀ����
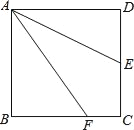
����Ŀ����ͼ����ֱ������ϵ�У���ABC�����BCA��90�㣬AC��BC��![]() ����A��C�ֱ���x���y���ϣ�����A��ԭ�㿪ʼ��x����������˶�ʱ�����Cʼ����y�����˶�����Bʼ���ڵ�һ�����˶���
����A��C�ֱ���x���y���ϣ�����A��ԭ�㿪ʼ��x����������˶�ʱ�����Cʼ����y�����˶�����Bʼ���ڵ�һ�����˶���
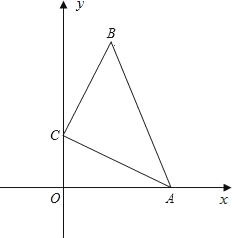
��1����AB��y��ʱ����B�����꣮
��2������A��C���˶�������B����ֱ��y��3x��ʱ�����ʱA������꣮
��3���ڣ�2���������£���y�����Ƿ���ڵ�D��ʹ��O��A��B��DΪ������ı��������4��������ڣ���ֱ��д����D�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1����B����Ϊ��![]() ��
��![]() ����2����A��2��0������3�����ڵ�D����D����Ϊ��0����1����0��2��.
����2����A��2��0������3�����ڵ�D����D����Ϊ��0����1����0��2��.
��������
��1�����ݹ��ɶ������ɵ�AB�ij������ݹ��ɶ������ɵ�AO�ij����ɵ�B�����ꣻ
��2������ȫ�������ε��ж������ʣ��ɵ�BE��OC��x��EC��OA��x�����ݹ��ɶ������ɵ�x�ij����ɵ�A�����ꣻ
��3���������ۣ���D��y����������ϣ���D��y��ĸ������ϣ���������ĺͲ�ɵù���y�ķ��̣����ݽⷽ�̣��ɵô𰸣�
��1���ߡ�BCA��90�㣬AC��BC��![]() ��
��
���BAC��45�㣬AB��![]() ��
��![]()
��AB��y�ᣬ
���BAO��90�㣽��COA
���CAO��45�㣽��OCA
��CO��AO
��AO2+CO2��AC2��
��2AO2��5
��AO��![]()
���B������![]() ��
��![]() ��
��
��2����ͼ������B����BE��y�ᣬ����Ϊ��E��
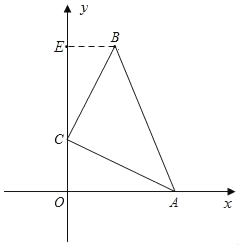
�ߡ�BCE+��ACO��90�㣬��ACO+��CAO��90��
���BCE����CAO����AC��BC����BEO����AOC
���AOC�ա�CEB��AAS��
��BE��CO��AO��CE
�ߵ�B����ֱ��y��3x��
����B��x��3x��
��BE��x��OC��OE��3x��
��CE��OA��2x��
��OA2+OC2��AC2
�ࣨ2x��2+x2��5
��x��1
��OA��2x��2
���A��2��0��
��3�����D��0��y��
����D��y���������ϣ���ͼ������OB��
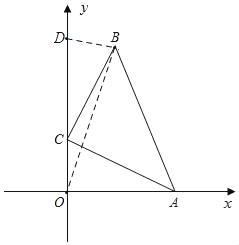
��S�ı���ABDO��S��AOB+S��BDO��4
��![]() ��y��1+
��y��1+![]() ��2��3��4
��2��3��4
��y��2
���D��0��2��
����D��y�Ḻ�����ϣ���ͼ������OB��

��S�ı���ABDO��S��AOB+S��ADO��4
��![]() ��2��3+
��2��3+![]() ��2������y����4
��2������y����4
��y����1
���D������0����1��.
����ڵ�D����D����Ϊ��0��2����0����1��.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�