题目内容

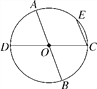
【题目】如图，在⊙O中，AB，CD是两条直径，弦CE∥AB，弧EC所对的圆心角的度数是40°，求∠BOD的度数．

【答案】110°

【解析】【试题分析】连接DE. DC是⊙O的直径，根据直径所对的圆周角是直角哦，得：∠DEC＝90°.因为弧EC所对的圆心角的度数是40°，同弧所对的圆周角是圆心角的一半，得：∠EDC＝20°，根据直角三角形两锐角互余，得：∠ECD＝70°.因为CE∥AB，两直线平行，内错角相等，得：∠AOD＝∠ECD＝70°，根据邻补角互补，得：∠BOD＝110°.

【试题解析】

连接DE.∵DC是⊙O的直径，∴∠DEC＝90°.

∵弧EC所对的圆心角的度数是40°，∴∠EDC＝20°，∴∠ECD＝70°.

∵CE∥AB，∴∠AOD＝∠ECD＝70°，∴∠BOD＝110°.

练习册系列答案
相关题目

【题目】非负数满足，设的最大值为，最小值为，则_______．

【题目】如图,在方格纸中，有两条线段AB，BC利用方格纸完成以下操作（保留作图痕迹）：

（1）过点A作BC的平行线；

（2）过点C作AB的平行线，与（1）中的平行线交于点D；

（3）过点B作AB的垂线，与（1）中的平行线交于点F.

【题目】如图，直线y=kx+2k（k≠0）与x轴交于点B，与双曲线交于点A、C，其中点A在第一象限，点C在第三象限．

（1）求B点的坐标；

（2）若S△AOB=2，求A点的坐标；

（3）在（2）的条件下，在y轴上是否存在点P，使△AOP是等腰三角形？若存在，请直接写出P点的坐标．

【题目】观察下面各图，寻找对顶角（不含平角）

（1）如图（1），图中共有________对不同的对顶角.

（2）如图（2），图中共有________对不同的对顶角.

（3）如图（3），图中共有________对不同的对顶角.

（4）研究（1）~（3）小题中直线条数与对顶角的对数之间的关系，若有条直线相交于一点，则可形成________对不同的对顶角.

（5）计算2013条直线相交于一点，则可形成________对不同的对顶角.

【题目】如图，在中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且，连接BF．

证明：；

当满足什么条件时，四边形AFBD是矩形？并说明理由．

【题目】下列各题计算正确的是 ( )

A. (ab﹣1)·(﹣4ab2)=﹣4a2b3﹣4ab2 B. (3x2+xy﹣y2)·3x2=9x4+3x3y﹣y2

C. (﹣3a)·(a2﹣2a+1)=﹣3a3+6a2 D. (﹣2x)·(3x2﹣4x﹣2)=﹣6x3+8x2+4x

【题目】如图所示在△ABC中，∠C=90°，AC=BC，AD平分∠CAB交BC于D，DE⊥BA于E，AB=6厘米，则△DEB的周长是_____厘米．

【题目】如图，是用图象反映的某地男女生身高生长速度y（厘米/年）与年龄x（岁）的对应关系．根据图象，有以下四个推断：

①13岁时，男生、女生的身高增长速度相同

②13岁以后，男生的身高增长速度比女生的身高增长速度快

③15岁时，男生、女生的身高增长速度达到最高值

④13岁以前，男生的身高增长速度比女生的身高增长速度快

其中合理的是（　　）

A.①②B.①③C.②④D.③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网