��Ŀ����
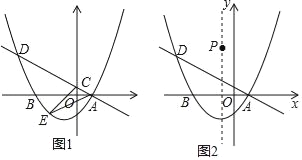
����Ŀ��ij������˾�Ŀ�ݳ��ͻ���ͬʱ�Ӽس������Ը��Ե��ٶ��������ҵ���ʻ����ݳ������ҵغ�������Ʒ����װ���ﹲ��45���ӣ�������ԭ·����һ�ٶ����ٷ��أ�ֱ���������������֪�������ٶ�Ϊ60ǧ��/ʱ������֮��ľ���y��ǧ�ף��������ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ���ش�һ������:

(1)��ס�������֮��ľ��룻
(2)���B�����ꣻ
(3)���ݳ����ҵط��ؼ�ʱ���ٶ�.
���𰸡���1���ס�������֮��ľ���Ϊ300km����2��B������Ϊ(3![]() ,75)����3����ݳ����ҵط��ؼ�ʱ���ٶ�Ϊ90km/h.
,75)����3����ݳ����ҵط��ؼ�ʱ���ٶ�Ϊ90km/h.
��������
��1����������ݳ����ٶ�=�������ٶ�+�������ٶȲ������������ݳ����ٶȣ��ٸ�����·��=��ݳ����ٶ�����ݳ������ҵص�ʱ�������ɵó����ۣ�
��2����Ͽ�ݳ�װ��45min���ɵó���B�ĺ����꣬������������ľ���=120-�����ٶ�����ݳ�װ��ʱ�������ɵó���B�������꣬�ɴ˼��ɵó���B�����ꣻ
��3����ϵ�B��C�ĺ�����ɵó���ݳ��ӷ��ص������������õ�ʱ�䣬�ٸ�������ݳ����ص��ٶ�=·����ʱ��-�������ٶ������ɵó����ۣ�
(1)��ݳ����ٶ�Ϊ��60+120��3=100(km/h)��
�ס�������֮��ľ���Ϊ��100��3=300(km).
�𣺼ס�������֮��ľ���Ϊ300km.
(2)��B�ĺ�����Ϊ��3+![]() =3
=3![]() (h)��
(h)��
��B����������120![]() ��60=75(km)��
��60=75(km)��
�ʵ�B������Ϊ(3![]() ,75).
,75).
(3)��ݳ��ӷ��ص������������õ�ʱ��Ϊ��4![]() (h)��
(h)��
��ݳ����ҵط��ؼ�ʱ���ٶ�Ϊ��75��![]() 60=90(km/h).
60=90(km/h).
�𣺿�ݳ����ҵط��ؼ�ʱ���ٶ�Ϊ90km/h.