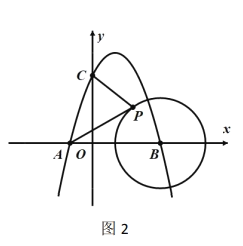Question

【题目】综合与实践 在中，，点为斜边上的动点(不与点重合)．

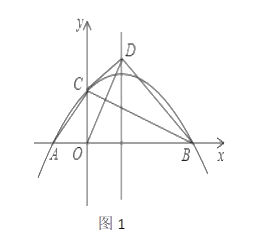
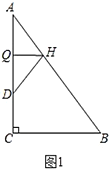
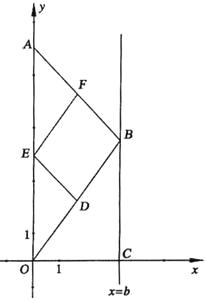
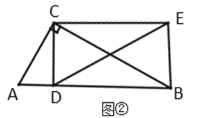
（1）操作发现： 如图①，当时，把线段绕点逆时针旋转得到线段，连接．

①的度数为________；

②当________时，四边形为正方形；

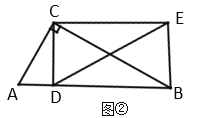
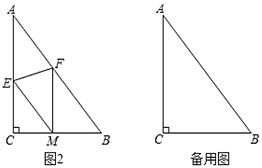
（2）探究证明： 如图②，当时，把线段绕点逆时针旋转后并延长为原来的两倍， 记为线段，连接．

①在点的运动过程中，请判断与的大小关系，并证明；

②当时，求证：四边形为矩形．

Answer 1

【答案】（1）①，②；（2）①；证明见解析；②见解析．

【解析】

（1）①由等腰三角形的性质得出∠A=∠ABC=45°，由旋转的性质得：∠ACD=∠BCE，CD=CE，证明△BCE≌△ACD，即可得出结果；

②由四边形为正方形，得BE=CD，∠CDB=90°，因为AC=BC，所以△ABC是等腰三角形，所以∠A=∠ABC=45°，解直角三角形可得CD的长，从而得到BE的长；

（2）①证明△ACD∽△BCE，即可得出；

②由垂直的定义得出，由得∠DBE=90°，因为，所以得到四边形CDBE为矩形.

解：（1）①∵∠ACB=90°，AC=BC

∴∠A=∠ABC=45°

由旋转的性质得：∠ACD=∠BCE，CD=CE

在△BCE和△ACD中，

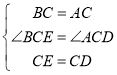
∴△BCE≌△ACD（SAS）

∴∠CBE=45°

②当BE=时，四边形为正方形.理由如下：

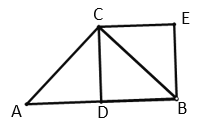
∵四边形为正方形

∴BE=CD，∠CDB=90°

∴CD⊥AB

∵AC=BC=8

∴△ABC是等腰三角形

∴∠A=∠ABC=45°

∴CD=ACsin45°=8×=4

∴BE=4

即当BE=时，四边形为正方形.

（2）①

证明：如图，

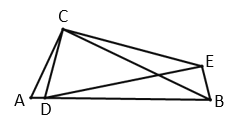
又

②证明：由（2）①得

又

四边形是矩形