题目内容
【题目】(1)发现:如图![]() ,点
,点![]() 是线段
是线段![]() 上的一点,分别以
上的一点,分别以![]() 为边向外作等边三角形
为边向外作等边三角形![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() ,
,![]() ,相交于点
,相交于点![]() .
.

①线段![]() 与
与![]() 的数量关系为:___________;
的数量关系为:___________;![]() 的度数为__________.
的度数为__________.
②![]() 可看作
可看作![]() 经过怎样的变换得到的?____________________________.
经过怎样的变换得到的?____________________________.
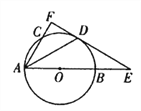
(2)应用:如图![]() ,若点
,若点![]() 不在一条直线上,(1)的结论①还成立吗?请说明理由;
不在一条直线上,(1)的结论①还成立吗?请说明理由;
(3)拓展:在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() ,
,![]() 两点之间的距离.
两点之间的距离.
【答案】(1)①![]() ,
,![]() ;(2)依然成立,见解析;(3)
;(2)依然成立,见解析;(3)![]() .
.
【解析】
(1)①证明△ABE≌△CBD,根据全等三角形的性质即可求出线段![]() 与
与![]() 的数量关系;根据三角形外角的性质即可求出
的数量关系;根据三角形外角的性质即可求出![]() 的度数.
的度数.
②根据旋转的性质即可求解.
(2)根据(1)①中的步骤进行证明即可.
(3)
解:(1)①∵△ABC和△BDE都是等边三角形,
∴AB=CB,EB=ED,![]()
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,

∴△ABE≌△CBD(SAS),
∴AE=CD,∠BAE=∠BCD,
由三角形的外角性质,∠AOC=∠BAE+∠BDC=∠BCD+∠BDC,
∠ABC=∠BCD+∠BDC,
∴∠AOC=∠ABC=![]() ;
;

故答案为:![]() ;
;![]() .
.
②![]() 可看作由
可看作由![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的(或
得到的(或![]() 可看作由
可看作由![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到)
得到)
(2)依然成立,理由如下:
∵![]() 和
和![]() 均是等边三角形,
均是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]()
在![]() 和
和![]() 中,
中,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
设![]() 与
与![]() 交于点
交于点![]()
∵![]() ,
,
∴![]()
在![]() 和
和![]() 中,其内角和均为
中,其内角和均为![]()
∵![]() ,
,
∴![]()
(3)将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,
,
根据旋转的性质可得:![]()
![]()
![]()
![]()
![]()

![]()

【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2=![]() [
[![]() ])
])