题目内容
【题目】如图,菱形ABCD和菱形ECGF的边长分别为4和6,∠A=120°,则阴影部分的面积是 . 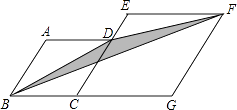
【答案】4 ![]()
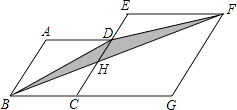
【解析】解:如图,设BF交CE于点H, ∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得CH= ![]() ,
,
所以,DH=CD﹣CH=4﹣ ![]() =
= ![]() ,
,
∵∠A=120°,
∴∠ECG=∠ABC=180°﹣120°=60°,
∴点B到CD的距离为4× ![]() =2
=2 ![]() ,
,
点G到CE的距离为6× ![]() =3
=3 ![]() ,
,
∴阴影部分的面积=S△BDH+S△FDH ,
= ![]() ×
× ![]() ×2
×2 ![]() +
+ ![]() ×
× ![]() ×3
×3 ![]() ,
,
=4 ![]() .
.
所以答案是:4 ![]() .
.
【考点精析】关于本题考查的菱形的性质,需要了解菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.

练习册系列答案
相关题目
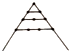
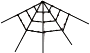
【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
名称及图形 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 | ||||
… | … | … | … | … |
第n层几何点数 |
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.