��Ŀ����
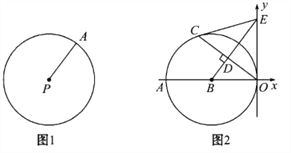
����Ŀ����ͼ��ʾ����֪������y��x2��bx��c��x�ύ��A��B���㣨��A�ڵ�B��ࣩ����y�ύ�ڵ�C(0��-3)���Գ�����ֱ��x��1��ֱ��BC�������ߵĶԳ��ύ�ڵ�D��
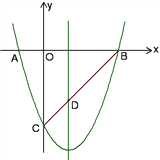
��1���������ߵĺ�������ʽ��
��2����ֱ��BC�ĺ�������ʽ��
��3����EΪy����һ���㣬CE�Ĵ�ֱƽ���߽�CE�ڵ�F������������P��Q���㣬�ҵ�P�ڵ������ޣ�
�ٵ��߶�PQ ![]() ʱ����tan��CED��ֵ��
ʱ����tan��CED��ֵ��
�ڵ���C��D��EΪ�������������ֱ��������ʱ����ֱ��д����P�����꣮
���ο���ʽ��������![]() �Ķ���������
�Ķ���������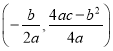 ��
��
���𰸡���1�������ߵĺ�������ʽΪ![]() ����2��ֱ��BC�ĺ�������ʽΪ
����2��ֱ��BC�ĺ�������ʽΪ![]() ����3����
����3����![]() ��
��![]() ��
�� 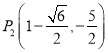 ��
��
�������������������1�����������ߵĶԳ��᷽�̿ɼ����b=-2���ٰ�C��0��-3�����������߽���ʽ�ɵõ�c=-3�����������ߵĺ�������ʽΪy=x2-2x-3��
��2��������������x��Ľ�������õ�A��-1��0����B��3��0����Ȼ�����ô���ϵ�������ֱ��BC�ĺ�������ʽ��
��3������AB=4��PQ=![]() AB=3�����������ߵĶԳ��Եõ�P���Q�����ֱ��x=1�Գƣ���P��-
AB=3�����������ߵĶԳ��Եõ�P���Q�����ֱ��x=1�Գƣ���P��-![]() ��-
��-![]() ��������F��0��-
��������F��0��-![]() ������FC=3-OF=
������FC=3-OF=![]() ������PQ��ֱƽ��CE�ڵ�F����CE=2FC=
������PQ��ֱƽ��CE�ڵ�F����CE=2FC=![]() ����D��1��-2��������D��DG��CE�ڵ�G����ͼ1����DG=1��CG=1������GE=CE=CG=
����D��1��-2��������D��DG��CE�ڵ�G����ͼ1����DG=1��CG=1������GE=CE=CG=![]() ��Ȼ����Rt��EGD�У��������еĶ�����⣻
��Ȼ����Rt��EGD�У��������еĶ�����⣻
����E��0��t�������������ľ��빫ʽ�õ�DE2=12+��t+2��2��CD2=12+��-2+3��2=2��EC2=��t+3��2��Ȼ��������ۣ�����CDE=90��ʱ��DE2+CD2=EC2����12+��t+2��2+2=��t+3��2������CED=90��ʱ��DE2+CE2=CD2����12+��t+2��2+��t+3��2=2������ECD=90��ʱ��CD2+CE2=DE2����2+��t+3��2=12+��t+2��2���ٷֱ�ⷽ�����tȷ��E�����꣬Ȼ����ݶ��κ���ͼ���ϵ����������ȷ��P�����꣮
���������
��1��������� �� ���
�� ���![]() ��
��
���������ߵĺ�������ʽΪ![]() ��
��
��2����![]() =0����
=0����![]() ��
��
����A(-1��0)��B(3��0)��
��ֱ��BC�ĺ�������ʽΪ![]() ��
��
�����B(3��0)�͵�C(0��-3)����![]()
���![]() ��
��
����ֱ��BC�ĺ�������ʽΪ![]() ��
��
��3������ͼ2��ʾ����ΪAB��4������PQ![]() ����ΪP��Q����ֱ��x��1�Գƣ�
����ΪP��Q����ֱ��x��1�Գƣ�
���Ե�P�ĺ�����Ϊ![]() �� ���Ե�P������Ϊ
�� ���Ե�P������Ϊ![]() ����F������Ϊ
����F������Ϊ![]() ��
��
���� ![]() ��
�� ![]() ��
��
���� ![]() ����E������Ϊ
����E������Ϊ![]() ��
��
ֱ��BC: ![]() �������ߵĶԳ���x��1�Ľ���D������Ϊ��1����2����
�������ߵĶԳ���x��1�Ľ���D������Ϊ��1����2����
����D��DH��y�ᣬ����ΪH�� ��Rt��EDH�У�DH��1�� ![]() ��
��
����tan��CED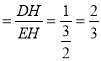 ��
��
����ͼ3��ͼ4�õ�P������Ϊ ![]() ��
�� 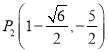 ��
��
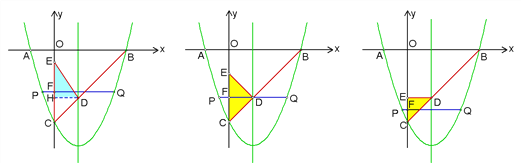
ͼ2 ͼ3 ͼ4
�㾦:�����Ƕ��κ������ۺ�����,�����漰����֪ʶ���������ߵĶ��㹫ʽ�������ε�������Լ��ô���ϵ������һ�κ����Ľ���ʽ�͵���ֱ�������ε�����,�����йض�������ʱҪע����������������۽��.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�