题目内容
【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
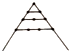
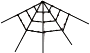
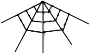
名称及图形 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 | ||||
… | … | … | … | … |
第n层几何点数 |
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
【答案】6;11;16;21;;2n﹣1;3n﹣2;4n﹣3
【解析】解:∵前三层三角形的几何点数分别是1、2、3,
∴第六层的几何点数是6,第n层的几何点数是n;
∵前三层正方形的几何点数分别是:1=2×1﹣1、3=2×2﹣1、5=2×3﹣1,
∴第六层的几何点数是:2×6﹣1=11,第n层的几何点数是2n﹣1;
∵前三层五边形的几何点数分别是:1=3×1﹣2、2=3×2﹣2、3=3×3﹣2,
∴第六层的几何点数是:3×6﹣2=16,第n层的几何点数是3n﹣2;
前三层六边形的几何点数分别是:1=4×1﹣3、5=4×2﹣3、9=4×3﹣3,
∴第六层的几何点数是:4×6﹣3=21,第n层的几何点数是4n﹣3.
名称及图形 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 | 6 | 11 | 16 | 21 |
… | … | … | … | … |
第n层几何点数 | n | 2n﹣1 | 3n﹣2 | 4n﹣3 |
故答案为:6、11、16、21、n、2n﹣1、3n﹣2、4n﹣3.
首先看三角形数,根据前三层的几何点数分别是1、2、3,可知第六层的几何点数是6,第n层的几何点数是n;然后看正方形数,根据前三层的几何点数分别是1=2×1-1,3=2×2-1,5=2×3-1,可知第六层的几何点数是2×6-1=11,可知第n层的几何点数是2n-1;再看五边形数,根据前三层的几何点数分别是1=3×1-2,4=3×2-1,7=3×3-2,可知第六层的几何点数是3×6-2=16,可知第n层的几何点数是3n-2;最后看六边形数,根据前三层的几何点数分别是1=4×1-3,5=4×2-3,9=4×3-3,可知第六层的几何点数是4×6-3=21,可知第n层的几何点数是4n-3;据此解答即可.